题目内容
设f(x)=a-
,其中a为常数;
(1)f(x)为奇函数,试确定a的值;
(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.
| 2 |
| 2x+1 |
(1)f(x)为奇函数,试确定a的值;
(2)若不等式f(x)+a>0恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:(1)由奇函数定义可得f(-x)=-f(x)恒成立,由此可得a值;
(2)f(x)+a>0恒成立,可化为2a>
恒成立,等价于2a>(
)max,利用基本函数的性质可求得(
)max;
(2)f(x)+a>0恒成立,可化为2a>
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
解答:
解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),即a-
=-a+
,
∴2a=
+
=
+
=2,
∴a=1;
(2)f(x)+a>0恒成立,即a-
+a>0,2a>
恒成立,等价于2a>(
)max,
而2x>0,2x+1>1,∴0<
<2,
故2a≥2,解得a≥1,
故实数a的取值范围[1,+∞).
∴f(-x)=-f(x),即a-
| 2 |
| 2-x+1 |
| 2 |
| 2x+1 |
∴2a=
| 2 |
| 2-x+1 |
| 2 |
| 2x+1 |
| 2•2x |
| 1+2x |
| 2 |
| 2x+1 |
∴a=1;
(2)f(x)+a>0恒成立,即a-
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
| 2 |
| 2x+1 |
而2x>0,2x+1>1,∴0<
| 2 |
| 2x+1 |
故2a≥2,解得a≥1,
故实数a的取值范围[1,+∞).
点评:本题考查奇函数的性质、恒成立问题,考查转化思想,恒成立常常转化为函数最值解决,熟记常见基本初等函数的有关性质可提高解题速度.

练习册系列答案
相关题目
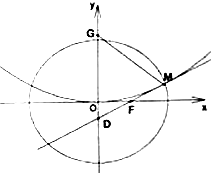 已知椭圆K
已知椭圆K