题目内容
已知函数f(x)=ax(a>0且a≠1)满足f(2)>f(3),若f-1(x)是f(x)的反函数,则关于x的不等式f-1(1-x)>1的解集是 .
考点:反函数
专题:函数的性质及应用
分析:由题意得到f(x)为减函数,利用指数函数的性质得到a大于0小于1,求出f(x)的反函数,将所求不等式变形后,即可求出解集.
解答:
解:∵函数f(x)=ax(a>0且a≠1)满足f(2)>f(3),
∴f(x)为减函数,即0<a<1,
∴y=f-1(x)=logax为减函数,
所求不等式变形得:loga(1-x)>1=logaa,
∴0<1-x<a,
解得:1-a<x<1,
则不等式的解集为{x|1-a<x<1}.
故答案为:(1-a,1)
∴f(x)为减函数,即0<a<1,
∴y=f-1(x)=logax为减函数,
所求不等式变形得:loga(1-x)>1=logaa,
∴0<1-x<a,
解得:1-a<x<1,
则不等式的解集为{x|1-a<x<1}.
故答案为:(1-a,1)
点评:此题考查了其他不等式的解法,涉及的知识有:反函数,指数、对数函数的性质,是一道基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知数列{an}为等差数列,a1∈(0,1),a2∈(1,2),a3∈(2,3),则a4的取值范围是( )
| A、(3,4) | ||||
B、(2
| ||||
| C、(3,9) | ||||
D、(
|
函数f(x)=
+
的定义域是( )
| x-1 |
| 4-x |
| A、∅ |
| B、(-∞,1)∪[4,+∞) |
| C、(1,4) |
| D、[1,4] |
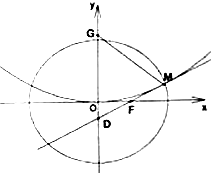 已知椭圆K
已知椭圆K