题目内容
已知M为椭圆
+
=1上一点,N为椭圆长轴上一点,O为坐标原点.给出下列结论:
①存在点M,N,使得△OMN为等边三角形;
②不存在点M,N,使得△OMN为等边三角形;
③存在点M,N,使得∠OMN=90°;
④不存在点M,N,使得∠OMN=90°.
其中,所有正确结论的序号是 .
| x2 |
| 4 |
| y2 |
| 3 |
①存在点M,N,使得△OMN为等边三角形;
②不存在点M,N,使得△OMN为等边三角形;
③存在点M,N,使得∠OMN=90°;
④不存在点M,N,使得∠OMN=90°.
其中,所有正确结论的序号是
考点:命题的真假判断与应用,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程,简易逻辑
分析:利用椭圆的简单几何性质,直接可判断①正确②错误,分情况讨论点M,N的位置,利用余弦定理判断cos∠OMN的取值范围,即可确定③错误,④正确.
解答:
解:∵过原点倾斜角为60°的直线一定与椭圆由交点,
∴假设y轴右侧的交点是M,
在长轴上取ON=OM,
则△OMN就是等边三角形.
故①正确,②错误;
若点M和点N在y轴两侧,
则∠OMN一定是锐角;
若点M和点N在y轴同侧,
不妨设为在y轴的右侧.
设点M(x,y),
则y2=3-
x2,且0<x<2.
由椭圆性质可知,
当点N是长轴短点时,∠OMN最大,
∵|OM|2=x2+y2,
|MN|2=(x-a)2+y2=(x-2)2+y2,
|ON|2=a2=4
∴|OM|2+|MN|2
=x2+y2+(x-2)2+y2
=2x2-4x+4+2y2
=
(x-4)2+2
在x∈(0,2)上上式恒小于4,
即|OM|2+|MN|2<|ON|2,
∴∠OMN<90°.
故③错误,④正确.
故答案为:①④.
∴假设y轴右侧的交点是M,
在长轴上取ON=OM,
则△OMN就是等边三角形.
故①正确,②错误;
若点M和点N在y轴两侧,
则∠OMN一定是锐角;
若点M和点N在y轴同侧,
不妨设为在y轴的右侧.
设点M(x,y),
则y2=3-
| 3 |
| 4 |
由椭圆性质可知,
当点N是长轴短点时,∠OMN最大,
∵|OM|2=x2+y2,
|MN|2=(x-a)2+y2=(x-2)2+y2,
|ON|2=a2=4
∴|OM|2+|MN|2
=x2+y2+(x-2)2+y2
=2x2-4x+4+2y2
=
| 1 |
| 2 |
在x∈(0,2)上上式恒小于4,
即|OM|2+|MN|2<|ON|2,
∴∠OMN<90°.
故③错误,④正确.
故答案为:①④.
点评:本题考查椭圆的几何性质的应用,直线与椭圆的位置关系,二次函数在固定区间上的最值等知识的综合应用.属于难题.

练习册系列答案
相关题目
函数f(x)=
+
的定义域是( )
| x-1 |
| 4-x |
| A、∅ |
| B、(-∞,1)∪[4,+∞) |
| C、(1,4) |
| D、[1,4] |
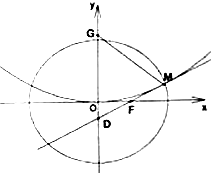 已知椭圆K
已知椭圆K