题目内容
已知数列{an}满足:a1=a,an+1=1+
.若
<an<2(n≥4),求a的取值范围.
| 1 |
| an |
| 3 |
| 2 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知条件,结合数列性质推导出当n≥4时,只需满足
<a4<2即可满足
<an<2,由此能求出a的取值范围.
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:∵
<an<2(n≥4),
∴
<
<
,
∴
<1+
<
<2,
∵a1=a,an+1=1+
,
∴
<an+1<2,(n≥4),
∴当n≥4时,只需满足
<a4<2即可满足
<an<2,
∴
<a4<2,
∵a2=1+
,a3=1+
=
,a4=1+
=
,
∴
<
<2,
解得a>0.
∴a的取值范围(0,+∞).
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| an |
| 2 |
| 3 |
∴
| 3 |
| 2 |
| 1 |
| an |
| 5 |
| 3 |
∵a1=a,an+1=1+
| 1 |
| an |
∴
| 3 |
| 2 |
∴当n≥4时,只需满足
| 3 |
| 2 |
| 3 |
| 2 |
∴
| 3 |
| 2 |
∵a2=1+
| 1 |
| a |
| 1 |
| a2 |
| a+2 |
| a+1 |
| 1 |
| a3 |
| 2a+3 |
| a+2 |
∴
| 3 |
| 2 |
| 2a+3 |
| a+2 |
解得a>0.
∴a的取值范围(0,+∞).
点评:本题考查数列中参数的取值范围的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合M={x|y2=3x,x∈R},N={y|x2+y2=4,x∈R,y∈R},则M∩N等于( )
A、{
| ||||
| B、[-2,2] | ||||
C、{(1,
| ||||
| D、[0,2] |
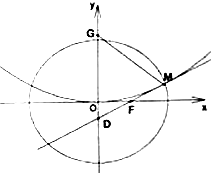 已知椭圆K
已知椭圆K