题目内容
F1、F2是椭圆
+y2=1的左右焦点,M是椭圆上一点,若
•
=0,则M到y轴的距离为( )
| x2 |
| 4 |
| MF1 |
| MF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意求可得MF1⊥MF2,利用三角形面积相等求M到x轴的距离为d.
解答:
解:由题意得,a=2,b=1,c=
;
∵
•
=0,
∴MF1⊥MF2,
∴MF12+MF22=(2
)2=12,
又∵MF1+MF2=4,
∴MF1×MF2=
=2,
设M到x轴的距离为d,
则2
×d=2,
则d=
.
故选C.
| 3 |
∵
| MF1 |
| MF2 |
∴MF1⊥MF2,
∴MF12+MF22=(2
| 3 |
又∵MF1+MF2=4,
∴MF1×MF2=
| 16-12 |
| 2 |
设M到x轴的距离为d,
则2
| 3 |
则d=
| ||
| 3 |
故选C.
点评:本题考查了椭圆的定义及其应用,也用到了三角形面积相等求高的方法,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
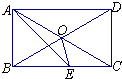 如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )
如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则以下结论:①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,⑤∠AEO=30°其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
在△ABC中,tanA=
,cosB=
,则sinC=( )
| 1 |
| 2 |
3
| ||
| 10 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、-2 |
已知直线l:2x+3y+1=0被圆C:x2+y2=1所截得的弦长为d,则下列直线中被圆C截得的弦长同样为d的直线是( )
| A、2x+4y-1=0 |
| B、2x+3y-1=0 |
| C、4x+3y-1=0 |
| D、3x+2y=0 |
已知向量
、
满足:|
|=2|
|=2
•
=2,若
-
与
-
的夹角等于
,则
•
的最大值为( )
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| π |
| 2 |
| c |
| a |
A、
| ||||
B、
| ||||
C、1+
| ||||
D、1+
|
下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
A、y=ln
| ||
| B、y=2-|x| | ||
| C、y=x2 | ||
| D、y=cosx |