题目内容
7.若三棱锥的三条侧棱两两垂直,且侧棱长均为$\sqrt{3}$,则三棱锥的体积与其外接球体积之比是$\frac{\sqrt{3}}{9π}$.分析 三棱锥为正三棱锥,利用勾股定理计算外接球的半径,代入体积公式求出三棱锥和外接球的体积即可得出体积比.
解答 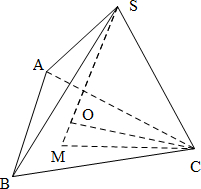 解:设三棱锥S-ABC,则SA,SB,SC两两垂直,SA=SB=SC=$\sqrt{3}$,
解:设三棱锥S-ABC,则SA,SB,SC两两垂直,SA=SB=SC=$\sqrt{3}$,
∴SA⊥平面SBC,
∴VS-ABC=VA-SBC=$\frac{1}{3}{S}_{△SBC}•SA$=$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×\sqrt{3}×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
∵SA=SB=SC=$\sqrt{3}$,且SA,SB,SC两两垂直,
∴AB=BC=AC=$\sqrt{6}$,即△ABC为等边三角形.
设△ABC的中心为O,连接OS,则OS⊥平面ABC,
设三棱锥外接球的球心为M,则M在直线OS上,
∵OC=$\frac{2}{3}$×$\frac{\sqrt{3}}{2}×\sqrt{6}$=$\sqrt{2}$,∴OS=$\sqrt{S{C}^{2}-O{C}^{2}}$=1,
设外接圆半径为r,则MS=MC=r,OM=r-1,
∵OM2+OC2=MC2,
∴(r-1)2+2=r2,解得r=$\frac{3}{2}$.
∴V外接球=$\frac{4}{3}π{r}^{3}$=$\frac{9π}{2}$.
∴$\frac{{V}_{S-ABC}}{{V}_{外接球}}$=$\frac{\sqrt{3}}{9π}$.
故答案为:$\frac{\sqrt{3}}{9π}$.
点评 本题考查了棱锥与外接球的关系,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
15.在等比数列{an}中a1=1,a4=64,则公比q的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
12.已知x,y取值如表:
y=0.95x+1.45为其回归直线,则m=1.8.
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | m | 5.6 | 6.1 | 7.4 | 9.3 |
19.对于数列{xn},若对任意n∈N*,都有$\frac{{x}_{n}+{x}_{n+2}}{2}$<xn+1成立,则称数列{xn}为“减差数列”.设bn=2t-$\frac{tn-1}{{2}^{n-1}}$,若数列b3,b4,b5,…是“减差数列”,则实数t的取值范围是( )
| A. | (-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | (-∞,1] |
16.已知数列{an}满足a1=0,an+1=$\frac{{{a_n}-2}}{{\frac{{5{a_n}}}{4}-2}}$,则a2014等于( )
| A. | 0 | B. | 2 | C. | $\frac{4}{3}$ | D. | 1 |