题目内容
19．对于数列{xn}，若对任意n∈N*，都有$\frac{{x}_{n}+{x}_{n+2}}{2}$＜xn+1成立，则称数列{xn}为“减差数列”．设bn=2t-$\frac{tn-1}{{2}^{n-1}}$，若数列b3，b4，b5，…是“减差数列”，则实数t的取值范围是（ ）| A． | （-1，+∞） | B． | （-∞，-1] | C． | （1，+∞） | D． | （-∞，1] |
分析 数列b3，b4，b5，…是“减差数列”，可得n≥3时，bn+bn+2＜2bn+1，代入化简即可得出．
解答 解：∵数列b3，b4，b5，…是“减差数列”，∴n≥3时，bn+bn+2＜2bn+1，
∴2t-$\frac{tn-1}{{2}^{n-1}}$+2t-$\frac{t（n+2）-1}{{2}^{n+1}}$＜2$（2t-\frac{t（n+1）-1}{{2}^{n}}）$，
化为：4（tn-1）+t（n+2）-1＞4t（n+1）-4，
∴t$＞\frac{1}{n-2}$，∵n≥3，∴$\frac{1}{n-2}$≤1，
∴t＞1．
∴实数t的取值范围是（1，+∞）．
故选：C．
点评 本题考查了新定义“减差数列”、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
10．设y=f（t）是某港口水的深度关于时间t（时）的函数，其中0＜t≤24，下表是该港口某一天从0至24时记录的时间t与水深y的关系．
经长期观察，函数y=f（t）的图象可以近似地看成函数y=k+Asin（ωt-φ）的图象．根据上述数据，函数y=f（t）的解析式为（ ）
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
| A． | y=12+3sin$\frac{πt}{6}$，t∈[0，24] | B． | y=12+3sin（$\frac{πt}{6}$+π），t∈[0，24] | ||
| C． | y=12+3sin$\frac{πt}{12}$，t∈[0，24] | D． | y=12+3sin（$\frac{πt}{12}$+$\frac{π}{2}$），t∈[0，24] |
11．已知sin（$\frac{π}{2}$-α）=$\frac{5}{13}$，且α是第四象限的角，则tan（2π-α）=（ ）
| A． | -$\frac{12}{5}$ | B． | $\frac{12}{5}$ | C． | ±$\frac{12}{5}$ | D． | ±$\frac{5}{12}$ |
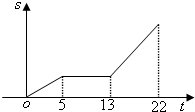某同学来学校上学，时间t（分钟）与路程s（米）的函数关系如图所示，现有如下几种说法：