题目内容
17．已知集合A={1，4，m}，集合B={1，m2}，若B⊆A，则实数m∈{0，2，-2}．分析 根据题意，若B⊆A，则有m2=m或m2=4解可得答案，注意最后进行集合元素互异性的验证．
解答 解：由B⊆A，
得到：①m2=m．解得m=1（舍）或0．
②m2=4，解得m=2或m=-2，
m=2，集合A={1，4，2}，集合B={1，4}，符合集合元素的互异性，B⊆A；
m=-2，集合A={1，4，-2}，集合B={1，4}，符合集合元素的互异性，B⊆A；
m=0，集合A={1，4，0}，集合B={1，0}，符合集合元素的互异性，B⊆A；
故答案为：{0，2，-2}．
点评 本题考查元素的互异性即集合间的关系，注意解题时要验证互异性．
练习册系列答案
阅读快车系列答案
相关题目
5．若一个函数恰有两个零点，则称这样的函数为“双胞胎”函数，若函数f（x）=|ax-lnx+$\frac{a-1}{x}$|-a-3（a＜0）为“双胞胎”函数，则实数a的取值范围为（ ）
| A． | （-$\frac{2}{3}$，+∞） | B． | （-∞，-$\frac{2}{3}$） | C． | （-$\frac{2}{3}$，0） | D． | （-1，-$\frac{2}{3}$） |
12．
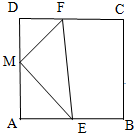如图，在正方形ABCD中，AB=2，点E、F分别在边AB、DC上，M为AD的中点，且$\overrightarrow{ME}•\overrightarrow{MF}$=0，则△MEF的面积的取值范围为（ ）
如图，在正方形ABCD中，AB=2，点E、F分别在边AB、DC上，M为AD的中点，且$\overrightarrow{ME}•\overrightarrow{MF}$=0，则△MEF的面积的取值范围为（ ）| A． | $[{1，\frac{5}{4}}]$ | B． | [1，2] | C． | $[{\frac{1}{2}，\frac{5}{4}}]$ | D． | $[{\frac{1}{2}，\frac{3}{2}}]$ |