题目内容
4.已知f(x)是定义在R上的偶函数,且在(-∞,0)上单调递增,a=f(0.80.8),b=f(0.81.6),c=f(1.60.8),则a,b,c的大小关系是( )| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | c<b<a |
分析 由条件即可得到f(x)在(0,+∞)上单调递减,而根据指数函数y=0.8x和y=1.6x的图象便可判断0.80.8,0.81.6,1.60.8这几个数的大小关系,从而由f(x)的单调性即可得出对应函数值的大小关系,即得出a,b,c的大小关系.
解答 解:根据条件知,f(x)在(0,+∞)上单调递减;
1>0.80.8>0.81.6,1.60.8>1;
∴1.60.8>0.80.8>0.81.6;
∴f(1.60.8)<f(0.80.8)<f(0.81.6);
即c<a<b.
故选:A.
点评 考查偶函数的定义,偶函数在对称区间上函数单调性的特点,根据指数函数的图象比较函数值大小的方法,以及减函数定义的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知命题p:x2-4x+3<0与q:x2-6x+8<0;若“p且q”是不等式2x2-9x+a<0成立的充分条件,则实数a的取值范围是( )
| A. | (9,+∞) | B. | {0} | C. | (-∞,9] | D. | (0,9] |
15.已知集合A={0,1,2},集合B={0,2,4},则A∩B=( )
| A. | {0,1,2} | B. | {0,2} | C. | {0,4} | D. | {0,2,4} |
19.函数$f(x)=\sqrt{4-2x}+{log_2}(x-1)$的定义域为( )
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | (1,2) |
16.正项等比数列{an}中,前n项和为Sn,若S4=30,a3+a5=40,则数列{an}的前9项和等于( )
| A. | 100 | B. | 1024 | C. | 1022 | D. | 16 |
13.下列函数中为奇函数的是( )
| A. | y=x•sinx | B. | y=x•cosx | C. | y=ln|x| | D. | y=2x-1 |
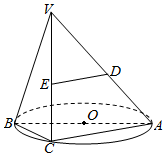 如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.
如图,AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D、E分别是VA、VC的中点.