题目内容
13.下列函数中为奇函数的是( )| A. | y=x•sinx | B. | y=x•cosx | C. | y=ln|x| | D. | y=2x-1 |
分析 根据奇函数、偶函数的定义及奇函数图象的对称性即可判断每个选项的函数的奇偶性,从而找出正确选项.
解答 解:A.定义域为R,且-xsin(-x)=xsinx;
∴该函数为偶函数;
B.定义域为R,且-xcos(-x)=-xcosx;
∴该函数为奇函数;
C.定义域为{x|x≠0},且ln|-x|=ln|x|;
∴该函数为偶函数;
D.y=2x-1的图象不关于原点对称,不是奇函数.
故选:B.
点评 考查奇函数和偶函数的定义,以及判断函数奇偶性的方法和过程,奇函数图象的对称性,指数函数的图象,以及图象沿y轴方向上的平移变换.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
4.已知f(x)是定义在R上的偶函数,且在(-∞,0)上单调递增,a=f(0.80.8),b=f(0.81.6),c=f(1.60.8),则a,b,c的大小关系是( )
| A. | c<a<b | B. | a<c<b | C. | a<b<c | D. | c<b<a |
18.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则2a+2c与2的大小关系是( )
| A. | 2a+2c>2 | B. | 2a+2c≥2 | C. | 2a+2c≤2 | D. | 2a+2c<2 |
2.函数y=f(x)是定义在R上的可导函数,则“y=f(x)是R上的增函数”是“f′(x)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.函数f(x)的导函数f′(x)的图象如图所示,则函数f(x)的解析式可能为( )
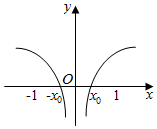

| A. | $\frac{{e}^{x}}{x}$ | B. | x2•lnx | C. | $\frac{{e}^{|x|}}{x}$ | D. | x•lnx2 |