题目内容
20.△ABC的三个内角满足:$\frac{sinB-sinA}{sinB-sinC}$=$\frac{c}{a+b}$,则∠A=( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
分析 已知等式左边利用正弦定理化简,整理后得到关系式,利用余弦定理表示出cosA,将得出关系式代入求出cosA的值,即可确定出∠A的度数.
解答 解:由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$化简已知等式得:$\frac{b-a}{b-c}$=$\frac{c}{a+b}$,
整理得:(b-a)(b+a)=c(b-c),即b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∵∠A为△ABC的内角,
∴∠A=$\frac{π}{3}$.
故选:B.
点评 此题考查了正弦、余弦定理,以及特殊角的三角函数值,熟练掌握正弦、余弦定理是解本题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
12.已知函数f(x)=sin(x+ϕ)为偶函数,则ϕ的取值可以为( )
| A. | $-\frac{π}{2}$ | B. | π | C. | $\frac{π}{3}$ | D. | 0 |
15.圆(x-a)2+(y-b)2=r2的圆心在x轴上,且与y轴相切,则下面关系中一定成立的是( )
| A. | a=0且b=0 | B. | b=0且r=|a| | C. | b=0且r=a | D. | b=0且r=-a |
5.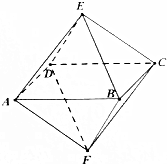 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
①不平行的两条棱所在的直线所成的角是60°或90°;
②四边形AECF是正方形;
③点A到平面BCE的距离为1.
其中正确的命题有( )
 如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:
如图,已知一个八面体的各条棱长均为1,四边形ABCD为正方形,给出下列命题:①不平行的两条棱所在的直线所成的角是60°或90°;
②四边形AECF是正方形;
③点A到平面BCE的距离为1.
其中正确的命题有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.空间四边形(四条边不在同一平面的四边形)中异面直线的对数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
9.已知点O是△ABC的外心,a、b、c分别为角A、B、C的对边,2c2-c+b2=0,则$\overrightarrow{BC}$•$\overrightarrow{AO}$的取值范围是( )
| A. | [-$\frac{1}{4}$,2) | B. | (-$\frac{1}{8}$,0) | C. | (-$\frac{1}{8}$,$\frac{1}{24}$] | D. | (0,$\frac{1}{3}$) |