题目内容
某个命题与正整数有关,若当n=k(k∈N*)时该命题成立,那么推得n=k+1时该命题成立,现已知当n=8时,该命题不成立,那么可推得( )
| A、当n=7时,该命题成立 |
| B、当n=7时,该命题不成立 |
| C、当n=9时,该命题成立 |
| D、当n=9时,该命题不成立 |
考点:数学归纳法
专题:点列、递归数列与数学归纳法,简易逻辑
分析:利用互为逆否命题的两个命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,于是可得到答案.
解答:
解:由题意可知,原命题成立则逆否命题成立,
P(n)对n=8不成立,P(n)对n=7也不成立,
否则n=7时命题成立,由已知必推得n=8也成立.
与当n=8时该命题不成立矛盾
故选:B.
P(n)对n=8不成立,P(n)对n=7也不成立,
否则n=7时命题成立,由已知必推得n=8也成立.
与当n=8时该命题不成立矛盾
故选:B.
点评:本题考查的知识点是数学归纳法,由归纳法的性质,考查互为逆否命题的两个命题同真同假的性质应用,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知双曲线
-
=1左、右焦点分别为F1,F2,过点F2作与x轴垂直的直线与双曲线一个交点为P,且∠PF1F2=
,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±x |
命题“若p则q”的逆否命题是( )
| A、若q则p |
| B、若¬p则¬q |
| C、若¬q则¬p |
| D、若p则¬q |
集合P={x,1},Q={y,1,2},其中x,y∈{1,2,3,4,5},则满足条件P⊆Q的事件的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在极坐标系中,方程ρ=2cosθ的图形是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
椭圆x2+4y2=1的离心率为( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
已知f(x)=sin(ωx+
)的图象与y=1的图象的两相邻交点间的距离为π,要得到y=f(x)的图象,只需把y=sinωx的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
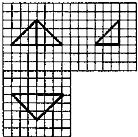 如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为
如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为