题目内容
20.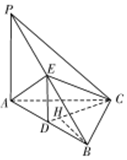 如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.
如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.(1)求证:BC⊥平面PAC;
(2)请作出点B在平面DEC上的射影H,并说明理由.若$BC=3,BH=\frac{12}{5}$,求三棱锥P-ABC的体积.
分析 (1)推导出DE⊥AB,PA⊥AB,从而PA⊥平面ABC,进而BC⊥PA,再由PC⊥BC,能证明BC⊥平面PAC.
(2)过点B作BH⊥CD于H,推导出H为点B在平面DEC上的射影,求出AB=5,PB=10,PA=5$\sqrt{3}$,由此能求出三棱锥P-ABC的体积.
解答 证明:(1)如图,∵△ABE是正三角形,且D为AB的中点,
∴DE⊥AB,
∵E为PB的中点,∴PA∥DE,∴PA⊥AB,
∵PA⊥AC,AB∩AC=A,
∴PA⊥平面ABC,∴BC⊥PA,
又∵PC⊥BC,PA∩PC=P,
∴BC⊥平面PAC.
解:(2)如图,过点B作BH⊥CD于H,
由(1)知DE⊥平面ABC,∴BH⊥DE,
又∵BH⊥CD,DE∩CD=D,∴BH⊥平面DEC,
∴H为点B在平面DEC上的射影,
在Rt△ABC中,设AC=x,则AB=$\sqrt{{x}^{2}+9}$,CD=$\frac{1}{2}AB=\frac{1}{2}\sqrt{{x}^{2}+9}$,
S△BCD=$\frac{1}{2}{S}_{△ABC}$=$\frac{1}{2}×\frac{1}{2}×3×x$=$\frac{3x}{4}$,
由${S}_{△BCD}=\frac{1}{2}{×CD×BH}_{\;}=\frac{3}{5}\sqrt{{x}^{2}+9}$,得$\frac{3x}{4}=\frac{3}{5}\sqrt{{x}^{2}+9}$,
解得x=4,
∴AB=5,PB=10,PA=5$\sqrt{3}$,
∴三棱锥P-ABC的体积V=$\frac{1}{3}{S}_{△ABC}•PA=\frac{1}{3}×\frac{1}{2}×4×3×5\sqrt{3}$=10$\sqrt{3}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查函数与方程思想、化归转化思想、数形结合思想,是中档题.

| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
| A. | [0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,1] | C. | [-1,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,0] |
| A. | $2\sqrt{5}-1$ | B. | $2\sqrt{5}$ | C. | 3 | D. | 4 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | 3 | D. | 9 |
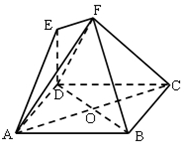 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.