题目内容
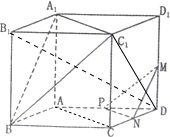
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.(1)求证:平面MNP∥平面A1C1B.
(2)将正方体沿平面A1C1B截出一个三棱锥B1-A1C1B,求次棱锥的体积与剩下的几何体体积的比.
(3)求直线B1D与直线MN所成的角.
考点:平面与平面平行的判定,异面直线及其所成的角
专题:证明题,空间位置关系与距离
分析:(1)通过证明AC∥A1C1,证明AC∥平面A1C1B,根据AC∥PN,可证PN∥平面A1C1B,同理MN∥平面A1C1B,由面面平行的判定定理得平面MNP∥平面A1C1B;
(2)计算截去的三棱锥的体积,可得截去的三棱锥的体积与剩下的几何体体积的比;
(3)先证DC1为DB1在平面CDD1C1内的射影,再根据三垂线定理证明MN⊥DB1,可得直线B1D与直线MN所成的角.
(2)计算截去的三棱锥的体积,可得截去的三棱锥的体积与剩下的几何体体积的比;
(3)先证DC1为DB1在平面CDD1C1内的射影,再根据三垂线定理证明MN⊥DB1,可得直线B1D与直线MN所成的角.
解答:
解:(1)证明:连接AC,∵AA1∥CC1,又AA1=CC1,
∴四边形ACC1A1为平行四边形,AC∥A1C1,AC?平面A1C1B,∴AC∥平面A1C1B,
又AC∥PN,∴PN∥平面A1C1B,
同理MN∥平面A1C1B,又MN∩PN=N,∴平面MNP∥平面A1C1B;
(2)VB1-A1C1B=
×
×a×a×a=
a3,
∴截去的三棱锥的体积与剩下的几何体体积的比为1:5;
(3)连接DC1,CD1,∵B1C1⊥平面CDD1C1,∴DC1为DB1在平面CDD1C1内的射影,
∵DC1⊥CD1,又MN∥CD1,由三垂线定理得:MN⊥DB1,
即直线B1D与直线MN所成的角为90°.
∴四边形ACC1A1为平行四边形,AC∥A1C1,AC?平面A1C1B,∴AC∥平面A1C1B,
又AC∥PN,∴PN∥平面A1C1B,
同理MN∥平面A1C1B,又MN∩PN=N,∴平面MNP∥平面A1C1B;
(2)VB1-A1C1B=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴截去的三棱锥的体积与剩下的几何体体积的比为1:5;
(3)连接DC1,CD1,∵B1C1⊥平面CDD1C1,∴DC1为DB1在平面CDD1C1内的射影,
∵DC1⊥CD1,又MN∥CD1,由三垂线定理得:MN⊥DB1,
即直线B1D与直线MN所成的角为90°.

点评:本题考查了线面平行,面面平行的判定,考查了异面直线所成角的求法及棱锥的体积计算,考查学生的空间想象能力与推理论证能力,熟练掌握线面平行,面面平行的判定定理及异面直线所成角的定义是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
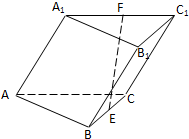 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为