题目内容
直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=
”是“△OAB的面积为
”的( )
| 3 |
| ||
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆,简易逻辑
分析:根据充分条件和必要条件的定义结合直线和圆的位置关系进行求解判断即可.
解答:
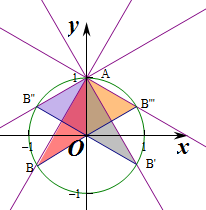
解:直线y=kx+1过定点(0,1)在圆上,不妨设A(0,1),
若“△OAB的面积为
”,
则S=
×12•sin∠AOB=
,
∴sin∠AOB=
,
即∠AOB=
或
,
若∠AOB=
,则直线的倾斜角为
或
,
若∠AOB=
,则直线的倾斜角为
或
,
若k=
,则直线的倾斜角为
,
故“k=
”是“△OAB的面积为
”的充分不必要条件,
故选:A
若“△OAB的面积为
| ||
| 4 |
则S=
| 1 |
| 2 |
| ||
| 4 |

∴sin∠AOB=
| ||
| 2 |
即∠AOB=
| π |
| 3 |
| 2π |
| 3 |
若∠AOB=
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
若∠AOB=
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
若k=
| 3 |
| π |
| 3 |
故“k=
| 3 |
| ||
| 4 |
故选:A
点评:本题主要考查充分条件和必要条件的应用,根据直线和圆相交对应三角形的面积求出对应直线的倾斜角是解决本题的关键.

练习册系列答案
相关题目
已知O是△ABC的外心,AB=6,AC=10,若
=x
+y
,且2x+10y=5,则△ABC的面积为( )
| AO |
| AB |
| AC |
| A、24 | ||||
B、
| ||||
C、18或
| ||||
D、24或20
|
从1,2,3,4,5这五个数中,随机取出两个数字,剩下三个数字的和是奇数的概率是( )
| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
