题目内容
设函数f(x)=cos(x-
)+2cos2
-1,x∈R.
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C所对应的边分别为a,b,c若f(B)=
,b=1,c=
求a的值.
| π |
| 3 |
| x |
| 2 |
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C所对应的边分别为a,b,c若f(B)=
| 3 |
| 3 |
考点:余弦定理,三角函数中的恒等变换应用
专题:三角函数的图像与性质,解三角形
分析:(1)由三角函数中的恒等变换应用化简解析式可得f(x)=
sin(x+
),由正弦函数的图象和性质可得f(x)的值域.
(2)由f(B)=
,可得sin(B+
)=1,由0<B<π,可求B的值,由余弦定理得a2-3a+2=0,即可解得a的值.
| 3 |
| π |
| 3 |
(2)由f(B)=
| 3 |
| π |
| 3 |
解答:
解:(1)f(x)=
cosx+
sinx+cosx=
sinx+
cosx=
sin(x+
),
故f(x)的值域为[-
,
]…(6分)
(2)由f(B)=
sin(x+
)=
,
∴sin(B+
)=1
又∵0<B<π,
∴B=
,
由余弦定理:b2=a2+c2-2accosB得a2-3a+2=0,解得a=1或a=2…(12分)
(注:第(2)问也可用正弦定理求解)
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
故f(x)的值域为[-
| 3 |
| 3 |
(2)由f(B)=
| 3 |
| π |
| 3 |
| 3 |
∴sin(B+
| π |
| 3 |
又∵0<B<π,
∴B=
| π |
| 6 |
由余弦定理:b2=a2+c2-2accosB得a2-3a+2=0,解得a=1或a=2…(12分)
(注:第(2)问也可用正弦定理求解)
点评:本题主要考查了三角函数中的恒等变换应用,考查了余弦定理在解三角形中的应用,属于基本知识的考查.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
下列类比中:
①与圆心距离相等的两弦相等:类比到空间:与球心距离相等的两个数面圆的面积相等;
②圆的面积S=πr2,类比到空间:球的体积为V=πr2;
③圆心与弦(垂直经)中点的连线垂直于弦,类比到空间,球心与截面圆(不经过球心的小截面圆)圆心的连线垂直与截图,
其中正确的类比是( )
①与圆心距离相等的两弦相等:类比到空间:与球心距离相等的两个数面圆的面积相等;
②圆的面积S=πr2,类比到空间:球的体积为V=πr2;
③圆心与弦(垂直经)中点的连线垂直于弦,类比到空间,球心与截面圆(不经过球心的小截面圆)圆心的连线垂直与截图,
其中正确的类比是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
已知f(x)=ex(sinx-cosx)(0≤x≤2015π),求则函数f(x)的各极大值之和为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=
”是“△OAB的面积为
”的( )
| 3 |
| ||
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
下列函数中,定义域和值域相同的是( )
| A、y=x2和y=2x |
| B、y=sinx和y=tanx |
| C、y=x3和y=log2x |
| D、y=x2和y=|x| |
某同学设计的算法流程图用以计算和式12+22+32+…+20152的值,则在判断框中应填写( )
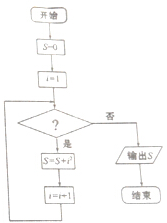

| A、i≤2015 |
| B、i≤2016 |
| C、≥2015 |
| D、i≥2016 |