题目内容
已知函数f(x)=
满足f(c2)=
.
(1)求常数c的值;
(2)求函数f(x)的值域.
|
| 9 |
| 8 |
(1)求常数c的值;
(2)求函数f(x)的值域.
考点:函数的值域,函数的值
专题:函数的性质及应用
分析:(1)由题意可得0<c<1,∴c2<1,则c2<c,把f(c2)=
代入分段函数即可求得c的值;
(2)把(1)中求得的c代入分段函数解析式,分段求出值域后取并集得答案.
| 9 |
| 8 |
(2)把(1)中求得的c代入分段函数解析式,分段求出值域后取并集得答案.
解答:
解:(1)由题意可知,0<c<1,∴c2<1,则c2<c,
∴f(c2)=c3+1=
,解得:c=
;
(2)由c=
,得f(x)=
,
当0<x<
时,得f(x)∈(1,
);
当
≤x<1时,得-4<-4x≤-2,f(x)∈(
,
].
综上,函数的值域为(1,
].
∴f(c2)=c3+1=
| 9 |
| 8 |
| 1 |
| 2 |
(2)由c=
| 1 |
| 2 |
|
当0<x<
| 1 |
| 2 |
| 5 |
| 4 |
当
| 1 |
| 2 |
| 17 |
| 16 |
| 5 |
| 4 |
综上,函数的值域为(1,
| 5 |
| 4 |
点评:本题考查了分段函数的值域及其求法,分段函数的值域要分段求,然后取并集,是中档题.

练习册系列答案
相关题目
若直线y=x+b与曲线y=
有两个交点,则实数b的取值范围是( )
| 4-x2 |
A、(2,2
| ||||
B、[2,2
| ||||
C、(-2,2
| ||||
D、(-2
|
已知f(x)=ex(sinx-cosx)(0≤x≤2015π),求则函数f(x)的各极大值之和为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
直线l:y=kx+1与圆O:x2+y2=1相交于A,B两点,则“k=
”是“△OAB的面积为
”的( )
| 3 |
| ||
| 4 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
某同学设计的算法流程图用以计算和式12+22+32+…+20152的值,则在判断框中应填写( )
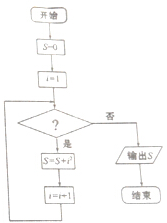

| A、i≤2015 |
| B、i≤2016 |
| C、≥2015 |
| D、i≥2016 |