题目内容
19．已知α 是第三象限角，$cosα=-\frac{12}{13}$，则tanα=$\frac{5}{12}$．分析 利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，先求得 sinα，进而求得tanα的值．
解答 解：∵α 是第三象限角，$cosα=-\frac{12}{13}$，∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{5}{13}$，
则tanα=$\frac{sinα}{cosα}$=$\frac{5}{12}$，
故答案为：$\frac{5}{12}$．
点评 本题主要考查同角三角函数的基本关系、以及三角函数在各个象限中的符号，属于基础题
练习册系列答案
相关题目
5．已知直线l过定点（0，1），则“直线l与圆（x-2）2+y2=4相切”是“直线l的斜率为$\frac{3}{4}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
7．已知命题p：?x＞0，都有logax＜0（a＞0且a≠1），命题q：?x∈Q，都有x∈R，则下列命题中为真命题的是（ ）
| A． | （￢p）∨q | B． | p∧q | C． | （￢p）∧（￢q） | D． | p∨（￢q） |
11．若椭圆的焦距与短轴长相等，则此椭圆的离心率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
8．如图所示y=sin（ωx+φ）的图象可以由y=sinωx的图象沿x轴经怎样的平移得到的（ ）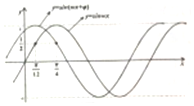
| A． | 沿x轴向左平移$\frac{π}{6}$个单位 | B． | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C． | 沿x轴向右平移$\frac{π}{6}$个单位 | D． | 沿x轴向右平移$\frac{π}{6}$个单位 |