题目内容
15．设直线m上有3个点，直线n上有6个点，则这9个点能确定1或9个平面．分析 根据平面的基本性质：直线及直线外一点可确定一个平面，对这9个点可确定平面的个数进行判断即可．
解答 解：由题意知本题是一个计数问题，
直线m，n共面时，这9个点能确定1个平面；
直线m，n异面时
∵从直线m上取一个点，这个点与直线n上的两个点可以确定平面，
但是它和直线n上的其他点确定的平面重合，故只有一个，
直线m上有3个点，可以确定3个平面，
同理直线n上的6个点可以确定6个平面，
根据分类计数原理知共有3+6=9个平面，
故答案为：1或9．
点评 本题是一个异面直线和计数问题结合的题目，是一个综合题，本题容易出的错误是不去掉哪些重复的平面，这是一个易错题．
练习册系列答案
相关题目
5．设a，b∈R，则“a＞b＞0”是“$\frac{1}{a}$$＜\frac{1}{b}$”的（ ）条件．
| A． | 充分而不必要 | B． | 必要而不充分 | ||
| C． | 充分必要 | D． | 既不充分也不必要 |
6．
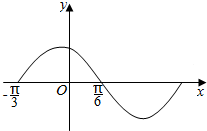函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）
函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示，如果x1，x2∈（-$\frac{π}{3}$，$\frac{π}{6}$），且f（x1）=f（x2），则f（x1+x2）等于（ ）| A． | -1 | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
4．$\sqrt{1-2sin（π+2）cos（π-2）}$等于（ ）
| A． | sin2-cos2 | B． | sin2+cos2 | C． | ±（sin2-cos2） | D． | cos2-sin2 |
1．下列函数中，在定义域内既是奇函数又是增函数的为（ ）
| A． | y=x+1 | B． | y=-$\frac{1}{x}$ | C． | y=-x|x| | D． | y=2x-2-x |