题目内容
2.已知x=1是函数f(x)=ax3-bx-lnx(a>0,b∈R)的一个极值点,则lna与b-1的大小关系是( )| A. | lna>b-1 | B. | lna<b-1 | C. | lna=b-1 | D. | 以上都不对 |
分析 求出f(x)的导数得到b=3a-1,作差令g(a)=lna-(b-1)=lna-3a+2,(a>0),根据函数的得到求出g(a)的最大值小于0,从而判断出lna和b-1的大小即可.
解答 解:f′(x)=3ax2-b-$\frac{1}{x}$,
∵x=1是f(x)的极值点,
∴f′(1)=3a-b-1=0,
即3a-1=b,
令g(a)=lna-(b-1)=lna-3a+2,(a>0),
则g′(a)=$\frac{1}{a}$-3=$\frac{1-3a}{a}$,
令g′(a)>0,解得:0<a<$\frac{1}{3}$,
令g′(a)<0,解得:a>$\frac{1}{3}$,
故g(a)在(0,$\frac{1}{3}$)递增,在($\frac{1}{3}$,+∞)递减,
故g(a)max=g($\frac{1}{3}$)=1-ln3<0,
故lna<b-1,
故选:B.
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | 16π-16 | B. | 8π-8 | C. | 16π-8 | D. | 8π-16 |
13.函数y=$\frac{\sqrt{x+1}}{x}$的定义域是( )
| A. | [-1,+∞) | B. | [-1,0) | C. | (-1,+∞) | D. | {x|x≥-1,且x≠0} |
10.已知函数y=2x+1,x∈{x∈Z|0≤x<3},则该函数的值域为( )
| A. | {y|1≤y<7} | B. | {y|1≤y≤7} | C. | {1,3,5,7} | D. | {1,3,5} |
7.设集合A={x|x2-4x+3≥0},B={x|2x-3≤0},则A∪B=( )
| A. | (-∞,1]∪[3,+∞) | B. | [1,3] | C. | $[{\frac{3}{2},3}]$ | D. | $({-∞,\frac{3}{2}}]∪[{3,+∞})$ |
11.已知命题p:若x<-3,则x2-2x-8>0,则下列叙述正确的是( )
| A. | 命题p的逆命题是:若x2-2x-8≤0,则x<-3 | |
| B. | 命题p的否命题是:若x≥-3,则x2-2x-8>0 | |
| C. | 命题p的否命题是:若x<-3,则x2-2x-8≤0 | |
| D. | 命题p的逆否命题是真命题 |
12.定义在R上的函数f(x),已知函数y=f(x+1)的图象关于直线x=-1对称,对任意的x1,x2∈(-∞,0)(x1≠x2),都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$,则下列结论正确的是( )
| A. | f(0.32)<f(20.3)<f(log25) | B. | $f({log_2}5)<f({2^{0.3}})<f({0.3^2})$ | ||
| C. | $f({log_2}5)<f({0.3^2})<f({2^{0.3}})$ | D. | $f({0.3^2})<f({log_2}5)<f({2^{0.3}})$ |
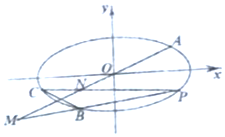 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.