题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求实数a的值.
(2)已知不等式f(logm
)+f(-1)>0恒成立,求实数m的取值范围.
| -2x+a |
| 2x+1 |
(1)求实数a的值.
(2)已知不等式f(logm
| 3 |
| 4 |
考点:函数恒成立问题,函数奇偶性的性质
专题:分类讨论,函数的性质及应用
分析:(1)由f(x)是R上的奇函数,得f(0)=0,求出a的值;
(2)由f(x)是R上的奇函数且是减函数,把不等式f(logm
)+f(-1)>0转化为logm
<logmm,再讨论m的取值,求出不等式成立的m的取值范围.
(2)由f(x)是R上的奇函数且是减函数,把不等式f(logm
| 3 |
| 4 |
| 3 |
| 4 |
解答:
解;(1)∵f(x)是R上的奇函数,
∴f(-x)=-f(x),
令x=0,则f(0)=0,
即
=
=0,
∴a=1,
∴f(x)=
;
(2)∵f(x)是R上的奇函数,
∴不等式f(logm
)+f(-1)>0
等价于f(logm
)>-f(-1)=f(1),
又∵f(x)=
=
=-1+
是R上的减函数,
∴logm
<1=logmm,
∴当0<m<1时,
>m,即0<m<
;
当m>1时,
<m,即m>1;
综上,m的取值范围是m∈(0,
)∪(1,+∞).
∴f(-x)=-f(x),
令x=0,则f(0)=0,
即
| -20+a |
| 20+1 |
| a-1 |
| 2 |
∴a=1,
∴f(x)=
| 1-2x |
| 1+2x |
(2)∵f(x)是R上的奇函数,
∴不等式f(logm
| 3 |
| 4 |
等价于f(logm
| 3 |
| 4 |
又∵f(x)=
| 1-2x |
| 1+2x |
| -2x-1+2 |
| 2x+1 |
| 2 |
| 1+2x |
∴logm
| 3 |
| 4 |
∴当0<m<1时,
| 3 |
| 4 |
| 3 |
| 4 |
当m>1时,
| 3 |
| 4 |
综上,m的取值范围是m∈(0,
| 3 |
| 4 |
点评:本题考查了函数的奇偶性与单调性的应用问题,也考查了对数函数的图象与性质的应用问题,是中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
定义某种运算⊙:S=a⊙b的算原理如框图,则式子5⊙3+2⊙4=( )

| A、14 | B、15 | C、16 | D、18 |
设数列{an}的前n项和为Sn,令Tn=
,则称Tn为数列a1,a2…,an,的“理想数”,已知数列a1,a2,…a20的“理想数”为2100,则15,a1,a2,…an的“理想数”为( )
| S1+S2+…+Sn |
| n |
| A、2013 | B、2014 |
| C、2015 | D、2016 |
命题p:幂函数y=x
在(-∞,0)上单调递减;命题q:已知函数f(x)=x3-3x2+m,若a,b,c∈[1,3],且f(a),f(b),f(c)能构成一个三角形的三边长,且4<m<8,则( )
| 2 |
| 3 |
| A、p且q为真命题 |
| B、p或q为假命题 |
| C、(¬p)且q为真命题 |
| D、p且(¬q)为真命题 |
一个几何体的三视图如图所示,则该几何体的底面积总和为( )
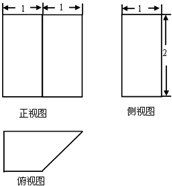

A、
| ||
| B、1 | ||
| C、3 | ||
| D、6 |