题目内容
若a，b，c∈R+，且
+
+
=1，则a+2b+3c的最小值为 ．
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 3c |
考点：基本不等式
专题：不等式的解法及应用
分析：利用“乘1法”和均值不等式即可得出．
解答：
解：∵a，b，c∈R+，且
+
+
=1，
∴a+2b+3c=（a+2b+3c）(
+
+
)≥3
•3
=9，
当且仅当a=2b=3c=3时取等号．
∴a+2b+3c的最小值为9．
故答案为：9．
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 3c |
∴a+2b+3c=（a+2b+3c）(
| 1 |
| a |
| 1 |
| 2b |
| 1 |
| 3c |
| 3 | 6abc |
| 3 |
| ||||||
当且仅当a=2b=3c=3时取等号．
∴a+2b+3c的最小值为9．
故答案为：9．
点评：本题考查了“乘1法”和均值不等式，属于基础题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
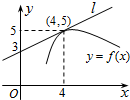如图，y=f（x）是可导函数，直线l是曲线y=f（x）在x=4处的切线，令g（x）=