题目内容
11.函数y=cos$\frac{x}{2}$的最小正周期是( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
分析 利用y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$,得出结论.
解答 解:函数y=cos$\frac{x}{2}$的最小正周期是$\frac{2π}{\frac{1}{2}}$=4π,
故选:D.
点评 本题主要考查余弦函数的周期性,利用了y=Acos(ωx+φ)的周期为$\frac{2π}{ω}$,属于基础题.

练习册系列答案
相关题目
1.已知集合A={x|ax2-5x+6=0},若2∈A,则集合A的子集个数为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
3.已知集合M={x|lg(x-2)≤0},N={x|-1≤x≤3},则M∪N=( )
| A. | {x|x≤3} | B. | {x|2<x<3} | C. | {x|-1≤x≤3} | D. | R |
20.在两坐标轴上截距均为m(m∈R)的直线l1与直线l2:2x+2y-3=0的距离为$\sqrt{2}$,则m=( )
| A. | $\frac{7}{2}$ | B. | 7 | C. | -1或7 | D. | -$\frac{1}{2}$或$\frac{7}{2}$ |
1.已知M={x|0<x<2},N={x|y=lg(x-1)},则M∩N=( )
| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|x>0} | D. | {x|x≥1} |
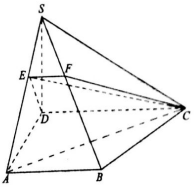 如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.
如图,在直角梯形ABCD中,∠ADC=∠BAD=90°,AB=AD=1,CD=2,平面SAD⊥平面ABCD,平面SDC⊥平面ABCD,SD=$\sqrt{3}$,在线段SA上取一点E(不含端点)使EC=AC,截面CDE交SB于点F.