题目内容
1.已知M={x|0<x<2},N={x|y=lg(x-1)},则M∩N=( )| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|x>0} | D. | {x|x≥1} |
分析 先分别求出集合M和N,由此能求出M∩N.
解答 解:∵M={x|0<x<2},N={x|y=lg(x-1)}={x|x>1},
∴M∩N={x|1<x<2}.
故选:B.
点评 本题考查交集的求法,是基础题,解题时要认真审题,注意交集定义的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.函数y=cos$\frac{x}{2}$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
9.P是双曲线C:$\frac{x^2}{2}-{y^2}$=1右支上一点,直线l是双曲线C的一条渐近线,P在l上的射影为Q,F1是双曲线C的左焦点,则|PF1|+|PQ|的最小值为( )
| A. | 1 | B. | $2+\frac{{\sqrt{15}}}{5}$ | C. | $4+\frac{{\sqrt{15}}}{5}$ | D. | $2\sqrt{2}+1$ |
6.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,出行健步不为难,次日脚疼减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一人走了378里路,第一天健步行走,从第二天起因脚疼每天走的路程为前一天的一半,走了6天后到达目的地.”问此人最后一天走了( )
| A. | 6里 | B. | 12里 | C. | 24里 | D. | 36里 |
11.抛物线y2=20x的焦点到准线的距离是( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
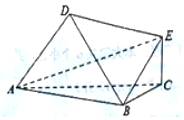 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2. 如图,给定由10个点(任意相邻两点距离为1,)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )
如图,给定由10个点(任意相邻两点距离为1,)组成的正三角形点阵,在其中任意取三个点,以这三个点为顶点构成的正三角形的个数是( )