题目内容
函数y=sin(
-2x)的单增区间为 .
| π |
| 4 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据正弦函数的单调性即可得到结论.
解答:
解:由y=sin(
-2x)=-sin(2x-
),
由2kπ+
≤2x-
≤2kπ+
,k∈Z,
即kπ+
≤x≤kπ+
,k∈Z,
故函数的递增区间为[kπ+
,kπ+
],k∈Z,
故答案为:[kπ+
,kπ+
],k∈Z
| π |
| 4 |
| π |
| 4 |
由2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
即kπ+
| 3π |
| 8 |
| 7π |
| 8 |
故函数的递增区间为[kπ+
| 3π |
| 8 |
| 7π |
| 8 |
故答案为:[kπ+
| 3π |
| 8 |
| 7π |
| 8 |
点评:本题主要考查三角函数单调区间的求解,利用正弦函数的图象和性质是解决本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
在等差数列{an}中,2a9=a12+6,则a6=( )
| A、6 | B、8 | C、10 | D、3 |
在下列根式中与分数指数幂的互化中,正确的是( )
A、(-x)0.5=-
| |||||||||
B、
| |||||||||
C、(
| |||||||||
D、x -
|
函数f(x)=2x2-mx+3,当x∈[-2,+∞)时,f(x)为增函数,当x∈(-∞,-2]时,函数f(x)为减函数,则m=( )
| A、-4 | B、-8 | C、8 | D、无法确定 |
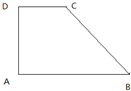 在如图所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,画出该梯形的直观图A′B′C′D′,并写出其做法(要求保留作图过程的痕迹.)
在如图所示直角梯形ABCD中,AB∥DC,∠A=90°,AB=AD=2DC=4,画出该梯形的直观图A′B′C′D′,并写出其做法(要求保留作图过程的痕迹.)