题目内容
二次函数f(x)=ax2+4(a+1)x-3在[2,+∞)上递减,则a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数的性质得出:当a<0,且-
≤2满足在[2,+∞)上递减,求解即可.
| 2(a+1) |
| a |
解答:
解:∵二次函数f(x)=ax2+4(a+1)x-3在[2,+∞)上递减,
∴当a<0,且-
≤2满足在[2,+∞)上递减,
∴求解得出a≤-
故答案为:a≤-
,
∴当a<0,且-
| 2(a+1) |
| a |
∴求解得出a≤-
| 1 |
| 2 |
故答案为:a≤-
| 1 |
| 2 |
点评:本题考查 了二次函数的性质,单调性,得出不等式求解即可,难度不大,属于中档题.

练习册系列答案
相关题目
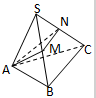 如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC
如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC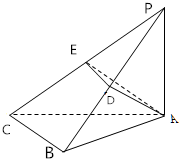 如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=
如图,PA⊥平面ABC,AB⊥BC,AD⊥PB,AE⊥PC,AP=