题目内容
8.在等比数列{an}中,a1=-2,a4=-54,则数列{an}的前n项和Sn=1-3n.分析 利用等比数列的通项公式和求和公式求解.
解答 解:∵等比数列{an}满足:a1=-2,a4=-54,
∴q3=27,解得q=3,
∴Sn=$\frac{-2(1-{3}^{n})}{1-3}$=1-3n.
故答案为:1-3n
点评 本题考查数列的前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
3.不等式|x+1|+|x-4|≥7的解集是( )
| A. | (-∞,-3]∪[4,+∞) | B. | [-3,4] | C. | (-∞,-2]∪[5,+∞) | D. | [-2,5] |
13.已知角θ的顶点与原点重合,始边与x轴非负半轴重合,终边过点P(-1,2),则cosθ=( )
| A. | -1 | B. | 2 | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
20.某四棱台的三视图如图所示,则该四棱台的侧面积是( )
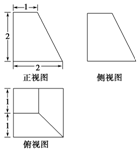

| A. | 12 | B. | $\frac{14}{3}$ | C. | $6+3\sqrt{5}$ | D. | $11+3\sqrt{5}$ |
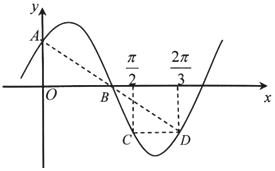 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.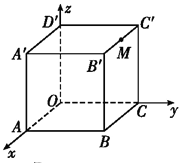 如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).
如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).