题目内容
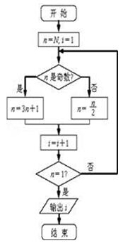
8.某次知识竞赛规则如下:在主办方预设固定顺序的5个题中,选手若能正确回答出3个题,即停止答题,晋级成功;否则需答满5个题.假设某选手正确回答每个问题的概率都是$\frac{2}{3}$,且每个题回答的正确与否都相互独立.(Ⅰ)求该选手连续答对3道题晋级的概率;
(Ⅱ)记该选手在竞赛中答对题的个数为X,求随机变量X的分布列和数学期望.
分析 (Ⅰ)设“该选手连续答对3道题晋级”的事件为A,
利用相互独立事件的概率公式求概率即可;
(Ⅱ)该选手在竞赛中答对题的个数为X,写出X的可能取值,
计算对应的概率值,写出X的分布列,求出数学期望值.
解答 解:(Ⅰ)设“该选手连续答对3道题晋级”的事件为A,
则P(A)=${(\frac{2}{3})}^{3}$+$\frac{1}{3}$×${(\frac{2}{3})}^{3}$+${(\frac{1}{3})}^{2}$×${(\frac{2}{3})}^{3}$=$\frac{104}{243}$;
(Ⅱ)该选手在竞赛中答对题的个数为X,则X的可能取值为0,1,2,3;
P(X=0)=${(\frac{1}{3})}^{5}$=$\frac{1}{243}$;
P(X=1)=${C}_{5}^{1}$×$\frac{2}{3}$×${(\frac{1}{3})}^{4}$=$\frac{10}{243}$;
P(X=2)=${C}_{5}^{2}$×${(\frac{2}{3})}^{2}$×${(\frac{1}{3})}^{3}$=$\frac{40}{243}$;
P(X=3)=${(\frac{2}{3})}^{3}$+${C}_{3}^{1}$×$\frac{1}{3}$×${(\frac{2}{3})}^{3}$+${C}_{4}^{2}$×${(\frac{1}{3})}^{2}$${×(\frac{2}{3})}^{3}$=$\frac{64}{81}$
(或P(X=3)=1-$\sum_{i=1}^{3}$P(X=i-1)=1-($\frac{1}{243}$+$\frac{10}{243}$+$\frac{40}{243}$)=$\frac{64}{81}$);
∴随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| p | $\frac{1}{243}$ | $\frac{10}{243}$ | $\frac{40}{243}$ | $\frac{64}{81}$ |
点评 本题考查了相互独立事件的概率以及离散型随机事件的分布列和数学期望值的计算问题,是中档题.

 阅读快车系列答案
阅读快车系列答案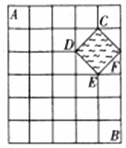 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.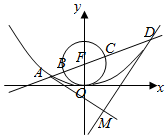 已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.
已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.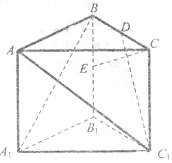 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.

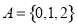 ,
,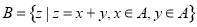 ,则
,则 ( )
( )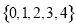 B.
B.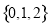 C.
C.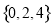 D.
D.