题目内容
已知x0,x0+
是函数f(x)=
sin(2ωx+φ)(ω>0,0<φ<
)的两个相邻的零点,函数与y轴相交于(0,
)
(1)求f(
)的值;
(2)若对任意x∈[-
,0),都有|f(x)-m|≤1,求实数m的取值范围.
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
| 3 |
| 4 |
(1)求f(
| π |
| 12 |
(2)若对任意x∈[-
| 7π |
| 12 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)条件三角函数的性质求出ω 和φ的值即可求f(
)的值;
(2)求出函数在x∈[-
,0)的取值范围,结合绝对值不等式的性质进行求解.
| π |
| 12 |
(2)求出函数在x∈[-
| 7π |
| 12 |
解答:
解:(1)∵x0,x0+
是函数f(x)=
sin(2ωx+φ)(ω>0,0<φ<
)的两个相邻的零点,
∴函数的周期T=2(x0+
-x0)=2×
=π,则
=π,
∴ω=1,
∵函数与y轴相交于(0,
),
∴f(0)=
sinφ=
,
即sinφ=
,
即φ=
,
则f(x)=
sin(2x+
),
即f(
)=
sin(2×
+
)=
sin
=
.
(2)∵f(x)=
sin(2x+
),
∴若x∈[-
,0),
则2x∈[-
,0),
2x+
∈[-
,
),
则-1≤sin(2x+
)<
,
则-
≤
sin(2x+
)<
,
即-
≤f(x)<
,
∴1-
≤1+f(x)<
,
-
<-1-f(x)≤-1-
,
若|f(x)-m|≤1,
则-1-f(x)≤m≤1+f(x),
即-1-
≤m≤1-
.
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
∴函数的周期T=2(x0+
| π |
| 2 |
| π |
| 2 |
| 2π |
| 2ω |
∴ω=1,
∵函数与y轴相交于(0,
| 3 |
| 4 |
∴f(0)=
| ||
| 2 |
| 3 |
| 4 |
即sinφ=
| ||
| 2 |
即φ=
| π |
| 3 |
则f(x)=
| ||
| 2 |
| π |
| 3 |
即f(
| π |
| 12 |
| ||
| 2 |
| π |
| 12 |
| π |
| 3 |
| ||
| 2 |
| π |
| 2 |
| ||
| 2 |
(2)∵f(x)=
| ||
| 2 |
| π |
| 3 |
∴若x∈[-
| 7π |
| 12 |
则2x∈[-
| 7π |
| 6 |
2x+
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
则-1≤sin(2x+
| π |
| 3 |
| ||
| 2 |
则-
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| 3 |
| 4 |
即-
| ||
| 2 |
| 3 |
| 4 |
∴1-
| ||
| 2 |
| 7 |
| 4 |
-
| 7 |
| 4 |
| ||
| 2 |
若|f(x)-m|≤1,
则-1-f(x)≤m≤1+f(x),
即-1-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查三角函数解析式的求解和求值,利用三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
数列{an}中,已知S1=1,S2=2,且Sn+1+2Sn-1=3Sn,(n≥2且n∈N*),则此数列为( )
| A、等差数列 |
| B、等比数列 |
| C、从第二项起为等差数列 |
| D、从第二项起为等比数列 |
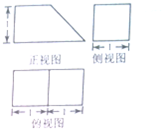
某几何体的三视图如图所示,则该几何体的体积胃( )

A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |
已知数列{an}满足a1=2,(n+1)•an+1=2(n+2)•an,若数列{an}的前n项和为Sn,则
=( )
| an+1 |
| Sn |
A、
| ||
B、
| ||
C、
| ||
D、
|