题目内容
已知数列{an}满足a1=1,an+1-an=2n(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)由a1=1,an+1-an=2n(n∈N*),利用累加法能求出数列{an}的通项公式.
(2)由bn=n•an=n•2n-n,利用错位相减法能求出数列{bn}的前n项和Sn.
(2)由bn=n•an=n•2n-n,利用错位相减法能求出数列{bn}的前n项和Sn.
解答:
解:(1)∵数列{an}满足a1=1,an+1-an=2n(n∈N*),
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+2+22+…+2n-1
=
=2n-1.
(2)∵bn=n•an=n•2n-n,
∴Sn=1•2+2•22+3•23+…+n•2n-(1+2+3+…+n),①
2Sn=1•22+2•23+3•24+…+n•2n+1-2(1+2+3+…+n),②
①-②,得:
-Sn=2+22+23+…+2n-n•2n+1+(1+2+3+…+n)
=
-n•2n+1+
=(1-n)•2n+1-2+
,
∴Tn=(n-1)•2n+1-
+2.
∴an=a1+a2-a1+a3-a2+…+an-an-1
=1+2+22+…+2n-1
=
| 1-2n |
| 1-2 |
=2n-1.
(2)∵bn=n•an=n•2n-n,
∴Sn=1•2+2•22+3•23+…+n•2n-(1+2+3+…+n),①
2Sn=1•22+2•23+3•24+…+n•2n+1-2(1+2+3+…+n),②
①-②,得:
-Sn=2+22+23+…+2n-n•2n+1+(1+2+3+…+n)
=
| 2(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
=(1-n)•2n+1-2+
| n(n+1) |
| 2 |
∴Tn=(n-1)•2n+1-
| n(n+1) |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,是中档题,解题时要认真审题,注意累加法和错位相减法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
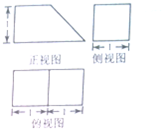
某几何体的三视图如图所示,则该几何体的体积胃( )

A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |