题目内容
13.已知向量$\overrightarrow{a}$=(0,1,1),$\overrightarrow{b}$=(-1,-1,0),则两向量的夹角为( )| A. | 60° | B. | 120° | C. | -60° | D. | 240° |
分析 根据向量的数量积,利用夹角公式求出两向量的夹角.
解答 解:向量$\overrightarrow{a}$=(0,1,1),$\overrightarrow{b}$=(-1,-1,0),
则$\overrightarrow{a}$•$\overrightarrow{b}$=0×(-1)+1×(-1)+1×0=-1,
|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{2}$;
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{-1}{\sqrt{2}×\sqrt{2}}$=-$\frac{1}{2}$,
∴两向量$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为120°.
故选:B.
点评 本题考查了空间向量的坐标表示与运算问题,也考查了求两向量的夹角大小的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知直线l过点P(3,-1),且与直线x+2y+2=0平行,则直线l的方程为( )
| A. | 2x+y-7=0 | B. | 2x-y-7=0 | C. | x+2y-5=0 | D. | x+2y-1=0 |
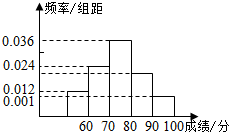 对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图:
对某班的全体学生一次数学测试成绩进行分析,数据的分组情况为:[50,60)[60,70)[70,80)[80,90)[90,100),频率分布直方图如图: