题目内容
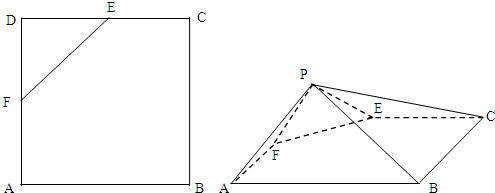
如图E,F是正方形ABCD的边CD、DA的中点,今将△DEF沿EF翻折,使点D转移至点P处,且平面PEF⊥平面ABCEF
(1)若平面PAF∩平面PBC=l,求证:l∥BC;
(2)求直线BC与平面PAB所成的角的正弦值.
(1)若平面PAF∩平面PBC=l,求证:l∥BC;
(2)求直线BC与平面PAB所成的角的正弦值.

考点:直线与平面所成的角,平面的基本性质及推论
专题:综合题,空间位置关系与距离
分析:(1)先证明AF∥平面PBC,再利用线面平行的性质证明l∥BC;
(2)利用VP-ABC=VC-PAB,求出C到平面PAB的距离,即可求直线BC与平面PAB所成的角的正弦值.
(2)利用VP-ABC=VC-PAB,求出C到平面PAB的距离,即可求直线BC与平面PAB所成的角的正弦值.
解答:
 (1)证明:∵AF∥BC,AF?平面PBC,BC?平面PBC,
(1)证明:∵AF∥BC,AF?平面PBC,BC?平面PBC,
∴AF∥平面PBC,
∵AF?平面PAF,平面PAF∩平面PBC=l,
∴l∥BC;
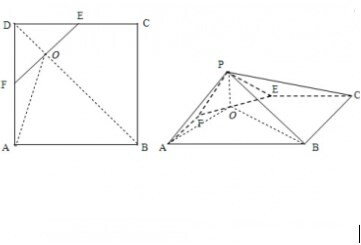
(2)解:设正方形的边长为2,则
取EF的中点O,连接OA,OB,则
PO=
,OB=
,OA=
,
∴PA=
,PB=
,
∴cos∠APB=
,
∴sin∠APB=
,
∴S△PAB=
×
×
×
=
设C到平面PAB的距离为h,
∵VP-ABC=VC-PAB,
∴
×
×2×2×
=
×
h,
∴h=
,
∴直线BC与平面PAB所成的角的正弦值
=
.
 (1)证明:∵AF∥BC,AF?平面PBC,BC?平面PBC,
(1)证明:∵AF∥BC,AF?平面PBC,BC?平面PBC,∴AF∥平面PBC,
∵AF?平面PAF,平面PAF∩平面PBC=l,
∴l∥BC;
(2)解:设正方形的边长为2,则
取EF的中点O,连接OA,OB,则
PO=
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
∴PA=
| 3 |
| 5 |
∴cos∠APB=
| 3+5-4 | ||||
2×
|
| 2 | ||
|
∴sin∠APB=
| ||
|
∴S△PAB=
| 1 |
| 2 |
| 3 |
| 5 |
| ||
|
| ||
| 2 |
设C到平面PAB的距离为h,
∵VP-ABC=VC-PAB,
∴
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
∴h=
2
| ||
|
∴直线BC与平面PAB所成的角的正弦值
| h |
| 2 |
| ||
| 11 |
点评:本题考查线面平行的判定与性质,考查直线BC与平面PAB所成的角的正弦值,正确运用线面平行的判定与性质,利用等体积计算C到平面PAB的距离是关键.

练习册系列答案
相关题目
函数y=
的定义域为( )
| ||
| x |
A、(-∞,
| ||
B、(-∞,
| ||
C、(0,
| ||
D、(-∞,0)∪(0,
|