题目内容
5.将函数$f(x)=2cos(x-\frac{π}{3})-1$的图象向右平移$\frac{π}{3}$个单位,再把所有的点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到函数y=g(x)的图象,则图象y=g(x)的一个对称中心为( )| A. | $(\frac{π}{6},0)$ | B. | $(\frac{π}{12},0)$ | C. | $(\frac{π}{6},-1)$ | D. | $(\frac{π}{12},-1)$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的图象的对称性,求得y=g(x)的一个对称中心.
解答 解:将函数$f(x)=2cos(x-\frac{π}{3})-1$的图象向右平移$\frac{π}{3}$个单位,可得y=2cos(x-$\frac{2π}{3}$)-1的图象;
再把所有的点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到函数y=g(x)=2cos(2x-$\frac{2π}{3}$)-1的图象,
令2x-$\frac{2π}{3}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{7π}{12}$,k∈Z,故图象y=g(x)的一个对称中心为($\frac{π}{12}$,-1),
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
16.设x∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a,则“a≤5”的概率为( )
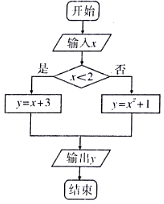

| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{5}{7}$ |
13.已知函数f(x)=x3+ax+1的图象在点(1,f(1))处的切线过点(2,7),则a=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
20.设F1、F2是双曲线C的两个焦点,若曲线C上存在一点P与F1关于曲线C的一条渐近线对称,则双曲线C的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |