题目内容
若直线x+y+2=0与圆x2+y2+2x-2y-4=0交于P，Q两点，则|PQ|=（ ）
| A、7 | B、6 | C、5 | D、4 |
考点：直线与圆相交的性质
专题：计算题,直线与圆
分析：确定圆心与半径，求出圆心（-1，1）到直线x+y+2=0的距离，利用勾股定理，即可求出|PQ|．
解答：
解：圆x2+y2+2x-2y-4=0，可化为（x+1）2+（y-1）2=6，
圆心（-1，1）到直线x+y+2=0的距离为
，
∴|PQ|=2
=4，
故选：D．
圆心（-1，1）到直线x+y+2=0的距离为
| 2 | ||
|
∴|PQ|=2
| 6-2 |
故选：D．
点评：本题考查直线与圆相交的性质，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
设椭圆的两个焦点分别为F1、F2，过F2作椭圆长轴的垂线交椭圆于点M，若△F1F2M为等腰直角三角形，则椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、2-
| ||||
D、
|
设变量x，y满足
，则x+y的最大值是（ ）
|
| A、1 | B、2 | C、3 | D、4 |
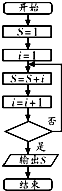阅读如图的程序框图（ 框图中的赋值符号“=”也可以写成“←”或“：=”），若输出S的值等于16，那么在程序框图中的判断框内应填写的条件是（ ）| A、i＞5？ | B、i＞6？ |
| C、i＞7？ | D、i＞8？ |