题目内容
2.已知点F为抛物线y2=2px(p>0)的焦点,点M(2,m)在抛物线E上,且|MF|=3.(1)求抛物线E的方程;
(2)求以点N(1,1)为中点的弦所在直线的方程.
分析 (1)利用抛物线的定义,求出p,即可求抛物线E的方程;
(2)设弦所在直线方程为 y-1=k(x-1),代入抛物线的方程,利用一元二次方程根与系数的关系,求出 k=2,从而得到弦所在直线方程.
解答 解:(1)由题意,2+$\frac{p}{2}$=3,∴p=2,
∴抛物线E的方程为y2=4x;
(2)由题意可得,弦所在直线斜率存在,设弦所在直线方程为 y-1=k(x-1),代入抛物线的方程可得
ky2-4y-4-4k=0,由 y1+y2=$\frac{4}{k}$=2 可得,k=2,
故弦所在直线方程为2x-y-1=0.
点评 本题考查抛物线的标准方程,考查用点斜式求直线方程的方法,一元二次方程根与系数的关系,求出k=2是解题的关键.

练习册系列答案
相关题目
1.2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
(${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.高二某班共有学生60人,座号分别为1,2,3,…,60现根据座号,用系统抽样的方法,抽取一个容量为5的样本.已知4号、28号、40号、52号同学在样本中,那么样本中还有一个同学的座号是( )
| A. | 14 | B. | 16 | C. | 36 | D. | 56 |
10.如果a<b<0,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a-c<b-c | C. | ac2<bc2 | D. | a2<b2 |
17.已知双曲线的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF2|=|F1F2|,且|QF2|=2|PF2|,则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{5}$ | D. | $\frac{8}{5}$ |
7.集合A={x∈N+|-1<x<4},B={x|x2≤4},则A∩B=( )
| A. | {0,1,2} | B. | {1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
14.已知函数f(x)=$\frac{\sqrt{5-ax}}{a-2}$(a∈A),若f(x)在区间(0,1]上是减函数,则集合A可以是( )
| A. | (-∞,0) | B. | [1,2) | C. | (-1,5] | D. | [4,6] |
11.已知θ∈(0,π),tanθ=-$\frac{3}{2}$,则cosθ=( )
| A. | $\frac{3}{{\sqrt{13}}}$ | B. | $-\frac{2}{{\sqrt{13}}}$ | C. | $\frac{2}{{\sqrt{13}}}$ | D. | $-\frac{3}{{\sqrt{13}}}$ |
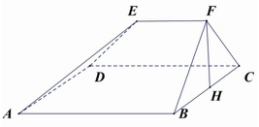 如图,多面体ABCDEF中,已知ABCD是边长为3的正方形,△FBC中BC边上的高为FH,EF⊥FH,EF∥AB,
如图,多面体ABCDEF中,已知ABCD是边长为3的正方形,△FBC中BC边上的高为FH,EF⊥FH,EF∥AB,