题目内容
在等比数列{an}中，已知a1=2，a2a3=32，则数列{an}的前6项和S6=（ ）
| A、62 | B、64 |
| C、126 | D、128 |
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由已知条件利用等比数列的通项公式得2q•2q2=4q3=32，求出q=2，由此能求出数列{an}的前6项和S6．
解答：
解：∵在等比数列{an}中，a1=2，a2a3=32，
∴2q•2q2=4q3=32，
解得q=2，
∴S6=
=
=126．
故选：C．
∴2q•2q2=4q3=32，
解得q=2，
∴S6=
| a1(1-q6) |
| 1-q |
| 2(1-26) |
| 1-2 |
故选：C．
点评：本题考查数列的前6项和的求法，是基础题，解题时要认真审题，注意等比数列的通项公式的合理运用．
练习册系列答案
相关题目
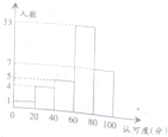某校为了了解新的一轮数改墨水有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图：
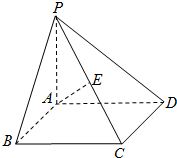如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知PA=AB=2，AD=2