题目内容
函数f（x）是定义域为R的奇函数，当x＞0时，f（x）=-x+1，则当x＜0时，f（x）=（ ）
| A、-x-1 | B、-x+1 |
| C、x+1 | D、x-1 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据题意，x＜0时，-x＞0，求出f（-x）的表达式，再利用奇函数求出f（x）的表达式．
解答：
解：∵函数f（x）是定义域为R的奇函数，且x＞0时，f（x）=-x+1，
∴当x＜0时，-x＞0，
∴f（-x）=-（-x）+1=x+1；
又f（-x）=-f（x），
∴-f（x）=x+1，
∴f（x）=-x-1．
故选：A．
∴当x＜0时，-x＞0，
∴f（-x）=-（-x）+1=x+1；
又f（-x）=-f（x），
∴-f（x）=x+1，
∴f（x）=-x-1．
故选：A．
点评：本题考查了利用函数的奇偶性求函数解析式的应用问题，是基础题目．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
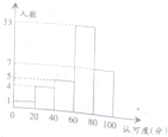某校为了了解新的一轮数改墨水有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图：