题目内容
设点P(3,2)是圆(x-2)2+(y-1)2=4内部一点,则以P为中点的弦所在的直线方程是有 .
考点:轨迹方程
专题:计算题,直线与圆
分析:求出圆的圆心与半径,求出所求直线的斜率,然后求解以点P为中点的弦所在的直线方程.
解答:
解:圆(x-2)2+(y-1)2=4的圆心(2,1),
点P(3,2)是圆(x-2)2+(y-1)2=4内部一点,
以点P为中点的弦所在的直线的斜率为:-
=-1.
以点P为中点的弦所在的直线方程为:y-2=-(x-3).
即x+y-5=0.
故答案为:x+y-5=0.
点P(3,2)是圆(x-2)2+(y-1)2=4内部一点,
以点P为中点的弦所在的直线的斜率为:-
| 3-2 |
| 2-1 |
以点P为中点的弦所在的直线方程为:y-2=-(x-3).
即x+y-5=0.
故答案为:x+y-5=0.
点评:本题考查直线与圆的位置关系,直线方程的求法,考查计算能力.

练习册系列答案
相关题目
若变量x,y满足约束条件
,则目标函数z=2x+y的最小值是( )
|
| A、6 | ||
| B、3 | ||
C、
| ||
| D、1 |
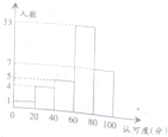 某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图:
某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图: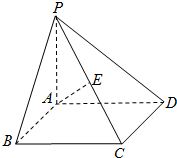 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知PA=AB=2,AD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知PA=AB=2,AD=2