题目内容
已知函数f(x)=|x-5|-|2x-2|+2.
(1)求f(x)的值域;
(2)关于x的不等式f(x)≤t+
,对t>0恒成立,求x的取值范围.
(1)求f(x)的值域;
(2)关于x的不等式f(x)≤t+
| 1 |
| t |
考点:绝对值不等式的解法,函数的值域
专题:不等式的解法及应用
分析:(1)化简函数f(x)的解析式,利用函数的单调性求出f(x)的值域.
(2)利用基本不等式可得f(x)≤2,数形结合求得此不等式的解集.
(2)利用基本不等式可得f(x)≤2,数形结合求得此不等式的解集.
解答:
 解:(1)函数f(x)=|x-5|-|2x-2|+2=
解:(1)函数f(x)=|x-5|-|2x-2|+2=
,故函数f(x)在(-∞,1)上是增函数,
f(x)在[1,+∞)上是减函数,
故当x=1时,函数f(x)取得最大值为f(1)=6,f(x)没有最小值,故函数f(x)的值域为(-∞,6].
(2)对t>0,则有t+
≥2,故有f(x)≤2.
令f(x)=2,求得x=-3,或x=
,数形结合求得f(x)≤2的解集为(-∞,-3]∪[
,+∞).
即要求的x的取值范围为(-∞,-3]∪[
,+∞).
 解:(1)函数f(x)=|x-5|-|2x-2|+2=
解:(1)函数f(x)=|x-5|-|2x-2|+2=
|
f(x)在[1,+∞)上是减函数,
故当x=1时,函数f(x)取得最大值为f(1)=6,f(x)没有最小值,故函数f(x)的值域为(-∞,6].
(2)对t>0,则有t+
| 1 |
| t |
令f(x)=2,求得x=-3,或x=
| 7 |
| 3 |
| 7 |
| 3 |
即要求的x的取值范围为(-∞,-3]∪[
| 7 |
| 3 |
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若数列{an}满足a1=2,an+1an=an-1,则a2013的值为( )
| A、-1 | ||
B、
| ||
| C、2 | ||
| D、3 |
已知球的直径为2,则球的表面积为( )
A、
| ||
| B、4π | ||
| C、8π | ||
| D、16π |
若变量x,y满足约束条件
,则目标函数z=2x+y的最小值是( )
|
| A、6 | ||
| B、3 | ||
C、
| ||
| D、1 |
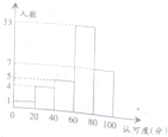 某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图:
某校为了了解新的一轮数改墨水有效性的“认可度”,在全校师生(可认为很多人)进行了“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”的问卷调查,现随机抽查50名师生,对他们的“认可度”统计分析得如图: