题目内容
14.已知函数y=ax在[-1,0]上的最大值与最小值的和为3.(1)求a的值.
(2)若1≤ax<16,求x的取值范围.
分析 (1)由指数函数的性质可得,y=ax在[-1,0]单调可得a-1+a0=3,可求,
(2)由指数函数的单调性质,即可求出x的范围.
解答 解:(1)由指数函数的性质可得,y=ax在[-1,0]单调,
∵函数y=ax在[-1,0]上的最大值与最小值的和为3,
∴a-1+a0=3
∴a=$\frac{1}{2}$,
(2)由(1)值,y=$(\frac{1}{2})^{x}$,
∵1≤ax<16,
∴$(\frac{1}{2})^{0}$=1≤$(\frac{1}{2})^{x}$<16=$(\frac{1}{2})^{-4}$,
∴-4<x≤0,.
点评 本题主要考查了指数函数的单调性的应用,属于基础试题,但若本题中给出的是最大值与最小值的差,就需要对a分a>1,0<a<1两种情况讨论了

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
4.定义在R上的偶函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,a,b是钝角三角形的两个锐角,则下列结论正确的是( )
| A. | f(sina)>f(cosb) | B. | f(sina)<f(cosb) | C. | f(cosa)<f(cosb) | D. | f(cosa)>f(cosb) |
5.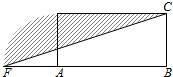 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
6.若a=log5$\frac{2}{3}$,b=log8$\sqrt{3}$,c=$\frac{1}{2}$log2$\sqrt{2}$,则a,b,c的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |