题目内容
4.定义在R上的偶函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,a,b是钝角三角形的两个锐角,则下列结论正确的是( )| A. | f(sina)>f(cosb) | B. | f(sina)<f(cosb) | C. | f(cosa)<f(cosb) | D. | f(cosa)>f(cosb) |
分析 由α,β是钝角三角形的两个锐角可得0°<a+b<90°即0°<a<90°-b,从而有0<sina<sin(90°-b)=
cosb<1,由f(x)满足f(2-x)=f(x)函数为偶函数即f(-x)=f(x)可得f(2-x)=f(x),即函数的周期为2,因为函数在[-3,-2]上是减函数,则根据偶函数的性质可得在[2,3]单调递增,根据周期性可知在0,1]单调递增,从而可判断.
解答 解:∵a,b是钝角三角形的两个锐角可得0°<a+b<90°即0°<a<90°-b,
∴0<sina<sin(90°-b)=cosb<1,
∵f(x)满足f(2-x)=f(x),∴函数关于x=1对称,
∵函数为偶函数即f(-x)=f(x)∴f(2-x)=f(x),即函数的周期为2,
∴函数在[-3,-2]上是减函数,则根据偶函数的性质可得在[2,3]单调递增,根据周期性可知在0,1]单调递增,
∴f(sina)<f(cosb),
故选:B.
点评 本题主要考查了函数的奇偶性、单调性等综合应用,解决的关键一是由f(2-x)=f(x),偶函数满足的f(-x)=f(x)可得函数的周期,关键二是要熟练掌握偶函数对称区间上的单调性相反的性质,关键三是要a,b是钝角三角形的两个锐角可得0°<a+b<90°即0°<a<90°-b.本题是综合性较好的试题.

练习册系列答案
相关题目
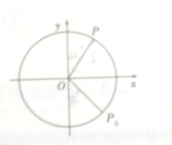 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0.
如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0($\sqrt{2}$,-$\sqrt{2}$),角速度为1,点P到x轴的距离d是关于时间t的函数,当t=$\frac{π}{4}$时,d=0. 已知函数f(x)=x|x-2|,
已知函数f(x)=x|x-2|,