题目内容
已知x,y∈R且
,则存在θ∈R,使得(x-4)cosθ+ysinθ+
=0的概率为( )
|
| 2 |
A、
| ||
B、
| ||
C、2-
| ||
D、1-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用辅助角公式将条件进行化简,求出对应的平面区域的面积即可得到结论.
解答:
 解:∵(x-4)cosθ+ysinθ+
解:∵(x-4)cosθ+ysinθ+
=0,
∴(4-x)cosθ-ysinθ=
,
即
cos(θ+β)=
,(β为参数),
∵存在θ∈R,使得(x-4)cosθ+ysinθ+
=0,
∴
≥
,
即(x-4)2+y2≥2,对应的图象是以(4,0)为圆心,半径r=
的圆的外部,
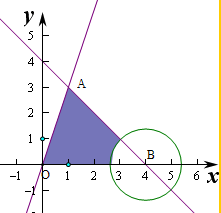
作出不等式组对应的平面区域如图,
则由
,解得
,即A(1,3),
则△AOB的面积S=
×4×3=6,
圆在△AOB内部的面积S=
×(
)2×
=
,
则(x-4)2+y2≥2,对应的区域面积S=6-
,
则对应的概率P=
=1-
,
故选:D.
 解:∵(x-4)cosθ+ysinθ+
解:∵(x-4)cosθ+ysinθ+| 2 |
∴(4-x)cosθ-ysinθ=
| 2 |
即
| (4-x)2+y2 |
| 2 |
∵存在θ∈R,使得(x-4)cosθ+ysinθ+
| 2 |
∴
| (4-x)2+y2 |
| 2 |
即(x-4)2+y2≥2,对应的图象是以(4,0)为圆心,半径r=
| 2 |
作出不等式组对应的平面区域如图,
则由
|
|
则△AOB的面积S=
| 1 |
| 2 |
圆在△AOB内部的面积S=
| 1 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
则(x-4)2+y2≥2,对应的区域面积S=6-
| π |
| 4 |
则对应的概率P=
6-
| ||
| 6 |
| π |
| 24 |
故选:D.
点评:本题主要考查几何概型的概率计算,根据三角函数的辅助角公式结合线性规划的知识是解决本题的关键.

练习册系列答案
相关题目
等比数列{an},满足a1=2,公比q=2,则a5=( )
| A、10 | B、16 | C、32 | D、64 |
已知数列{an}满足an+an+1=
(n∈N*),其中a1=-
,试通过计算a2,a3,a4,a5,猜想an等于( )
| (-1)n+1 |
| 2 |
| 1 |
| 2 |
A、an=
| |||||||||
B、an=-
| |||||||||
C、an=
| |||||||||
D、
|
△ABC中,a、b、c分别是角A、B、C的对边长,若a、b、c成等比数列,且a2=(a+c-b)•c,则角A等于( )
| A、30° | B、45° |
| C、60° | D、120° |
为了得到函数y=sin(
x-
)的图象,只需将y=sin
x图象上的每个点纵坐标不变,横坐标( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 已知,如图,在梯形ABCD中,AD∥BC,AD=3,BC=7,点M,N分别是对角线BD,AC的中点,则MN=( )
已知,如图,在梯形ABCD中,AD∥BC,AD=3,BC=7,点M,N分别是对角线BD,AC的中点,则MN=( )| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
已知动点P(t,t),Q(10-t,0),其中0<t<10,则点M(6,1),N(4,5)与直线PQ的关系是( )
| A、M,N均在直线PQ上 |
| B、M,N均不在直线PQ上 |
| C、M不在直线PQ上,N可能在直线PQ上 |
| D、M可能在直线PQ上,N不在直线PQ上 |
已知{an}为等差数列,{bn}为正项等比数列,公比q≠1,若a1=b1,a15=b15,则( )
| A、a8≥b8 |
| B、a8>b8 |
| C、a8≤b8 |
| D、a8<b8 |
定义一种新运算:a?b=
,已知函数f(x)=(1+
)?3log2(x+1),若方程f(x)-k=0恰有两个不相等的实根,则实数k的取值范围为( )
|
| 2 |
| x |
| A、(-∞,3) |
| B、(1,3) |
| C、(-∞,-3)∪(1,3) |
| D、(-∞,-3)∪(0,3) |