题目内容

在边长为a的正方形内随机取一个点，则此点落在该正方形的内切圆内部的概率为（　　）
A、
π
4
B、
π
6
C、
2
π
D、
3
π
考点：几何概型
专题：概率与统计
分析：由于正方形的边长为a，则内切圆半径为
a
2
，然后求出正方形面积及其内切圆的面积，代入几何概型公式，即可得到答案．
解答： 解：∵正方形的边长为a，
∵正方形的面积S正方形=a2
其内切圆半径为
a
2
，内切圆面积S圆=πr2=
a2
4
π，
故向正方形内撒一粒豆子，则豆子落在圆内的概率P=
a2π
4
a2
=
π
4
；
故选A．
点评：本题主要考查了几何概型，以及圆与正方形的面积的计算，解题的关键是弄清几何测度，属于基础题．
练习册系列答案
相关题目
设x，y满足约束条件
y≤x
y≥2-x
y≥3x-6
，则
3y-2x+7
x-2
的取值范围是
 
．
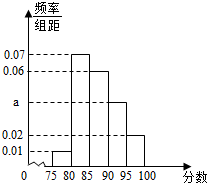某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩，
按成绩分成5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示．
（1）求a的值；
（2）若该校决定从第3，4组中用分层抽样的方法抽取5名学生进入第二轮面试，并从这5名学生中随机抽取2名学生接受综合素质测试．求第4组中恰有一名学生接受综合素质测试的概率．
若将函数f（x）=x5表示为f（x）=a0+a1（x-1）+a2（x-1）2+a3（x-1）3+a4（x-1）4+a5（x-1）5，其中a0，a1，a2，…a5为实数，则a1+a2+a3+a4+a5=
 
．
从[0，1]之间任意选出两个数，这两个数的平方和不大于1的概率是
 
．
甲乙两班进行一门课程的考试，按照学生考试成绩的优秀和不优秀统计后得到如列联表：
（1）据此数据有多大的把握认为学生成绩优秀与班级有关？
（2）用分层抽样的方法在成绩优秀的学生中随机抽取5名学生，问甲、乙两班各应抽取多少人？
（3）在（2）中抽取的5名学生中随机选取2名学生介绍学习经验，求至少有一人来自乙班的概率．（k2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d）
优秀不优秀总计
甲班153550
乙班104050
总计2575100
P（k2＞k）0.500.400.250.150.100.050.0250.0100.0050.001
k0.4550.7081.3232.0722.7063.8415.0246.6357.87910.828
设点M、N分别是不等边△ABC的重心与外心，已知A（0，1），B（0，-1），且
MN
=λ
AB
．
（1）求动点C的轨迹E；
（2）（理科）若直线y=kx+b与曲线E交于不同的两点P、Q，且满足
OP
•
OQ
=0，求实数b的取值范围．
（文科）若直线y=x+b与曲线E交于不同的两点P、Q，且满足
OP
•
OQ
=0，求实数b的取值．
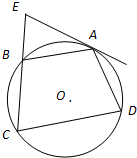如图，四边形ABCD的外接圆为⊙O，EA是⊙O的切线，CB的延长线与EA相交于点E，AB=AD．求证：AB2=BE•CD．
设t为实数，|
e1
|=2，|
e2
|=1，
e1
，
e2
的夹角为
π
3
，若向量2t
e1
+7
e2
与向量
e1
+t
e2
的夹角为钝角，则实数t的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网