题目内容
14.已知数列{an}的前n项和为Sn,满足${S_n}=2{a_n}-{2^n}(n∈{N^*})$.(1)证明$\{\frac{a_n}{2^n}\}$是等差数列,并求{an}的通项公式;
(2)求数列{an}的前n项和Sn.
分析 (1)根据数列的递推公式可得$\{\frac{a_n}{2^n}\}$是以$\frac{1}{2}$公差,以1为首项的等差数列,求出an即可,
(2)根据Sn=2an-2n,即可数列{an}的前n项和Sn.
解答 解:(1)证明:a1=S1=2a1-2,
∴a1=2,
∵Sn=2an-2n,
当n≥2时,Sn-1=2an-1-2n-1,
∴an=Sn-Sn-1=2an-1+2n-1,
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{1}{2}$,
∴$\{\frac{a_n}{2^n}\}$是以$\frac{1}{2}$公差,以1为首项的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=1+$\frac{1}{2}$(n-1)=$\frac{1}{2}$(n+1),
∴an=(n+1)2n-1,
(2)∵Sn=2an-2n,
∴Sn=2(n+1)2n-1-2n=n-2n.
点评 本题考查了数列的递推公式和等差数列的通项公式的求法和数列的前n项,属于中档题

练习册系列答案
相关题目
4.在数列{an}中,a1=1,$({n^2}+2n)({a_{n+1}}-{a_n})=1(n∈{N^*})$,则通项公式an=$\frac{7}{4}-\frac{2n+1}{2n(n+1)}$.
5.若函数f(x)=(x2-$\frac{3}{2}$x)ex-m有三个零点,则实数m的取值范围是( )
| A. | (0,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$) | B. | (-$\frac{e}{2}$,0] | C. | ($\frac{9}{2}$e${\;}^{-\frac{3}{2}}$,+∞) | D. | (-$\frac{e}{2}$,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$] |
2.如图,网格上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积为( )
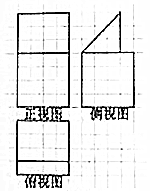

| A. | 93+12$\sqrt{2}$ | B. | 97+12$\sqrt{2}$ | C. | 105+12$\sqrt{2}$ | D. | 109+12$\sqrt{2}$ |
9.若a>3,则方程x3-ax2+1=0在区间(0,2)上的实根个数是( )
| A. | 3 个 | B. | 2 个 | C. | 1个 | D. | 0个 |
3. 某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )
某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )
 某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )
某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )| A. | 48 | B. | 54 | C. | 60 | D. | 64 |
4.教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲、乙两个同轨班级进行实验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面2×2列联表:(单位:人)
(1)能否据此判断有97.5%的把握认为加强语文阅读理解训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学题所用的时间在5-7分钟,小刚正确解答一道数学题所用的时间在6-8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们的大题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 优秀人数 | 非优秀人数 | 总计 | |
| 甲班 | 22 | 8 | 30 |
| 乙班 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(2)经过多次测试后,小明正确解答一道数学题所用的时间在5-7分钟,小刚正确解答一道数学题所用的时间在6-8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的8名同学中任意抽取两人,并对他们的大题情况进行全程研究,记A、B两人中被抽到的人数为X,求X的分布列及数学期望E(X).
附表及公式
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,与x轴交于A、B两点,与y轴交于P点,其一条对称轴与x轴交于C点,且PA=PC=2$\sqrt{3}$,PB=BC.则ω=$\frac{π}{4}$.