题目内容
5.若函数f(x)=(x2-$\frac{3}{2}$x)ex-m有三个零点,则实数m的取值范围是( )| A. | (0,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$) | B. | (-$\frac{e}{2}$,0] | C. | ($\frac{9}{2}$e${\;}^{-\frac{3}{2}}$,+∞) | D. | (-$\frac{e}{2}$,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$] |
分析 函数f(x)=(x2-$\frac{3}{2}$x)ex-m有三个零点,即:方程(x2-$\frac{3}{2}$x)ex=m有三个根,令g(x)=(x2-$\frac{3}{2}$x)ex,利用导数求出函数g(x)单调性,结合图象即可求解.
解答 解:函数f(x)=(x2-$\frac{3}{2}$x)ex-m有三个零点,即:方程(x2-$\frac{3}{2}$x)ex=m有三个根,
令g(x)=(x2-$\frac{3}{2}$x)ex,
∴g′(x)=ex(x2+$\frac{1}{2}$x-$\frac{3}{2}$)=0,∴x=1或x=-$\frac{3}{2}$,
∴当x∈(-∞,-$\frac{3}{2}$)时,g(x)单调递增,
当x∈(-$\frac{3}{2}$,1)时,g(x)单调递减,当x∈(1,+∞)时,g(x)单调递增;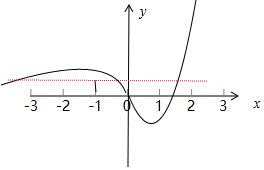
∴x=-$\frac{3}{2}$时,g(x)max=g(-$\frac{3}{2}$)=$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$,
x=1时,g(x)min=g(1)=-$\frac{1}{2}$e-1,
结合图象可得m∈(0,$\frac{9}{2}$e${\;}^{-\frac{3}{2}}$),
故选:A
点评 本小题主要考查函数的单调性、极值、最值等基本知识,考查运用导数研究函数性质的方法,考查运算能力,考查函数与方程、数形结合、分类与整合等数学思想方法和分析问题、解决问题的能力,属于中档题,

练习册系列答案
相关题目
16. 设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )
 设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),若y=(1-x)f′(x)的图象如图所示,则下列结论成立的是( )| A. | 函数f(x)有极大值f(-2)和极小值f(2) | B. | 函数f(x)有极大值f(-3)和极小值f(1) | ||
| C. | 函数f(x)有极大值f(-3)和极小值f(3) | D. | 函数f(x)有极大值f(3)和极小值f(-2) |
13.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y-a2=0与该圆的位置关系是( )
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 相切或相交 |
20.在极坐标系中,若过点A(3,0)且与极轴垂直的直线交曲线ρ=4cosθ于A、B两点,则|AB|=( )
| A. | $2\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
17.设向量$\overrightarrow{a}$=(x-1,x),$\overrightarrow{b}$=(x+2,x-4),则“$\overrightarrow{a}$⊥$\overrightarrow{b}$”是“x=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |