题目内容
10.有下列命题:①若函数f(x)=3sin(ωx+φ)对于任意的x都有f($\frac{π}{6}$+x)=-f($\frac{π}{6}$-x),则f($\frac{π}{6}$)=0;
②正切函数在定义域上单调递增;
③曲线g(x)=x2与曲线f(x)=2x有三个公共点;
④若$\overrightarrow{a}$∥$\overrightarrow{b}$,则有且只有一个实数λ,使$\overrightarrow{b}$=λ$\overrightarrow{a}$;
⑤已知函数f(x)=$\left\{\begin{array}{l}{sin(\frac{π}{2}x)-1,x<0}\\{lo{g}_{a}x(a>0,a≠1),x>0}\end{array}\right.$的图象上关于y轴对称的点至少有3对,则实数a的取值范围是(0,$\frac{\sqrt{5}}{5}$).
其中正确命题的序号是①③⑤.
分析 运用正弦函数的对称性,即可判断①;由正切函数的单调区间即可判断②;
令h(x)=x2-2x,可得h(2)=h(4)=0,再由零点存在定理,可得h(x)在x<0有一个零点,即可判断③;
运用向量共线定理,即可判断④;画出f(x)关于y轴对称的图象,设g(x)=-sin($\frac{π}{2}$x)-1,x>0,
通过图象观察,可得0<a<1且满足g(5)<f(5),解不等式即可判断⑤.
解答 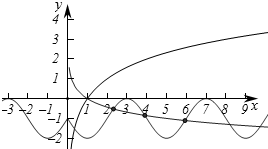 解:对于①,若函数f(x)=3sin(ωx+φ)对于任意的x都有f($\frac{π}{6}$+x)=-f($\frac{π}{6}$-x),
解:对于①,若函数f(x)=3sin(ωx+φ)对于任意的x都有f($\frac{π}{6}$+x)=-f($\frac{π}{6}$-x),
即有f(x)的图象关于点($\frac{π}{6}$,0)对称,则f($\frac{π}{6}$)=0,故①正确;
对于②,由正切函数的性质,可得正切函数在(kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$),k∈Z单调递增,故②错误;
对于③,令h(x)=x2-2x,可得h(2)=h(4)=0,h(-1)>0,h(0)<0,且h(x)在(-1,0)递减,
即有h(x)在(-1,0)有一个零点,故曲线g(x)=x2与曲线f(x)=2x有三个公共点正确;
对于④,若$\overrightarrow{a}$∥$\overrightarrow{b}$,($\overrightarrow{a}$≠$\overrightarrow{0}$),则有且只有一个实数λ,使$\overrightarrow{b}$=λ$\overrightarrow{a}$;若$\overrightarrow{a}$=$\overrightarrow{0}$,则λ有无数个,故④错误;
对于⑤,若x>0,则-x<0,
∵x<0时,f(x)=sin($\frac{π}{2}$x)-1,
∴f(-x)=sin(-$\frac{π}{2}$x)-1=-sin($\frac{π}{2}$x)-1,
则若f(x)=sin($\frac{π}{2}$x)-1,(x<0)关于y轴对称,
则f(-x)=-sin($\frac{π}{2}$x)-1=f(x),
即y=-sin($\frac{π}{2}$x)-1,x>0,
设g(x)=-sin($\frac{π}{2}$x)-1,x>0,
作出函数g(x)的图象,
要使y=-sin($\frac{π}{2}$x)-1,x>0与f(x)=logax,x>0的图象至少有3个交点,
则0<a<1且满足g(5)<f(5),即-2<loga5,即loga5>logaa-2,则5<$\frac{1}{{a}^{2}}$,
解得0<a<$\frac{\sqrt{5}}{5}$,故⑤正确.
故答案为:①③⑤.
点评 本题考查三角函数的图象和性质,考查函数的零点的判断和向量共线定理的运用,考查对数函数的图象的性质,属于中档题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| 甲 | 6 | 6 | 9 | 9 |
| 乙 | 7 | 9 | x | y |
(Ⅱ)如果x=y=7,从甲、乙两人的4局比赛中随机各选取1局,记这2局的得分和为X,求X的分布列和数学期望;
(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | 2或$\frac{1}{2}$ |