题目内容
14.四棱锥P-ABCD的底面ABCD是边长为6的正方形,且PA=PB=PC=PD,若一个半径为1的球与此四棱锥所有面都相切,则该四棱锥的高是$\frac{9}{4}$.分析 由球的球心在四棱锥P-ABCD的高上,把空间问题平面化,作出过正四棱锥的高作组合体的轴截面,利用平面几何知识即可求出高
解答 解:由题意,四棱锥P-ABCD是正四棱锥,球的球心O在四棱锥的高PH上;
过正四棱锥的高作组合体的轴截面如图所示:
其中PE,PF是斜高,A为球面与侧面的切点,
设PH=h,由几何体可知,RT△PAO∽RT△PHF⇒$\frac{OA}{FH}=\frac{OP}{FP}$
∴$\frac{h-1}{\sqrt{{h}^{2}+3}}=\frac{1}{3}$,解得h=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$
点评 题主要考查了球内切多面体、几何体的结构特征,把空间问题平面化,是解题的关键.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.等差数列{an}共有2n+1项,其中奇数项之和为319,偶数项之和为290,则其中间项为( )
| A. | 28 | B. | 29 | C. | 30 | D. | 31 |
6.在△ABC中,a=$\sqrt{3}$,A=120°,b=1,则角B的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
18.用反证法证明命题“若a2+b2≠0,则a,b不全为0(a,b∈R)”时,其假设正确的是( )
| A. | a,b中至少有一个为0 | B. | a,b中至少有一个不为0 | ||
| C. | a,b全为0 | D. | a,b中只有一个不为0 |
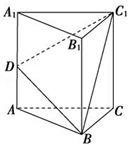 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=$\sqrt{3}$,则球O的体积等于$\frac{9π}{2}$.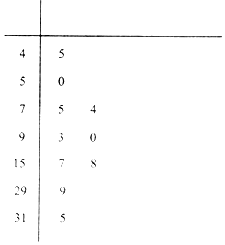 近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下:
近年来,空气质量成为人们越来越关注的话题,空气质量指数(AirQualityIndex,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的AQI的茎叶图如下: