题目内容
设函数f（x）=x3-3x2+2
（1）求函数f（x）的单调区间；
（2）若函数y=f（x）-m在区间[-2，4]上有三个零点，求实数m的取值范围．
（1）求函数f（x）的单调区间；
（2）若函数y=f（x）-m在区间[-2，4]上有三个零点，求实数m的取值范围．
考点：利用导数研究函数的单调性,利用导数研究函数的极值
专题：导数的综合应用
分析：（1）求导数f′（x），在定义域内解不等式f′（x）＞0，f′（x）＜0可求；
（2）求得f（x）的极值，利用数形结合即可得到结论．
（2）求得f（x）的极值，利用数形结合即可得到结论．
解答：
解：（1）由f（x）=x3-3x2+2，得f′（x）=3x2-6x=3x（x-2），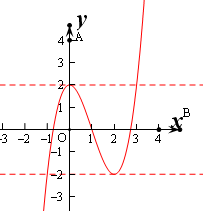
当f′（x）＞0时，解得x＜0或x＞2；
当f′（x）＜0时，解得0＜x＜2．
故函数f（x）的单调递增区间是（-∞，0），（2+∞））；
单调递减区间是（0，2）．
（2）由（1）知函数f（x）的单调递增区间是（-∞，0），（2+∞））；
单调递减区间是（0，2）．
∴函数在[-2，0）上递增，在[0，2]上递减，在[2，4]上递增，
且函数在x=0处取得极大值f（0）=2，在x=2处取得极小值f（2）=-2，
∵f（4）=18，f（-2）=-18，
若函数y=f（x）-m在区间[-2，4]上有三个零点，
等价为f（x）=m有三个不同的根
则有-2＜m＜2，故实数m的取值范围（-2，2）．
当f′（x）＞0时，解得x＜0或x＞2；
当f′（x）＜0时，解得0＜x＜2．
故函数f（x）的单调递增区间是（-∞，0），（2+∞））；
单调递减区间是（0，2）．
（2）由（1）知函数f（x）的单调递增区间是（-∞，0），（2+∞））；
单调递减区间是（0，2）．
∴函数在[-2，0）上递增，在[0，2]上递减，在[2，4]上递增，
且函数在x=0处取得极大值f（0）=2，在x=2处取得极小值f（2）=-2，
∵f（4）=18，f（-2）=-18，
若函数y=f（x）-m在区间[-2，4]上有三个零点，
等价为f（x）=m有三个不同的根
则有-2＜m＜2，故实数m的取值范围（-2，2）．
点评：该题考查利用导数研究函数的单调性、极值、函数的零点，考查不等式的求解，考查学生综合运用知识解决问题的能力
练习册系列答案
ABC考王全优卷系列答案
相关题目
在⊙O中，直径AB，CD互相垂直，BE切⊙O于B，且BE=BC，CE交AB于F，交⊙O于M，连结MO并延长，交⊙O于N，则下列结论中，正确的是（ ）| A、CF=FM |
| B、OF=FB |
| C、弧BM的度数为22.5° |
| D、BC∥MN |
已知
，
，
均为单位向量，且|
+
|=1，则（
-
）•
的取值范围是（ ）
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| A、[0，1] | ||||
| B、[-1，1] | ||||
C、[-
| ||||
D、[0，
|
如图，铁路线上AB段长100千米，工厂C到铁路的距离CA为20千米．现要在AB上某一点D处，向C修一条公路，已知铁路每吨千米的运费与公路每吨千米的运费之比为3：5．为了使原料从供应站B运到工厂C的运费最少，D点应选在何处？
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD的中点，M是棱PC上的点，PA=PD=AD=2BC=2，CD=
如图，在直角梯形ABCD中，∠A=∠D=90°，AB＜CD，SD⊥平面ABCD，AB=AD=a，SD=
攀枝花市欢乐阳光节是攀枝花市的一次向外界展示攀枝花的盛会，为了搞好接待工作，组委会在某大学招募了8名男志愿者和5名女志愿者（分成甲乙两组），招募时志愿者的个人综合素质测评成绩如图所示．