题目内容
已知定点 ,过点F且与直线
,过点F且与直线 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.
(I)求曲线E的方程;
(II)若点A的坐标为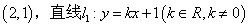 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线 于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
于点S,T.试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
解:(Ⅰ)由题意, 点 到点
到点 的距离等于它到直线
的距离等于它到直线 的距离, 故点
的距离, 故点 的轨迹是以点
的轨迹是以点 为焦点,
为焦点,  为准线的抛物线.
为准线的抛物线.
∴曲线 的方程为
的方程为 .
.
(Ⅱ)设点 的坐标分别为
的坐标分别为 ,依题意得,
,依题意得, .
.
由 消去
消去 得
得 ,
,
∴ 直线
直线 的斜
的斜 ,
,
故直线 的方程为
的方程为 .
.
令 ,得
,得 ,
,
∴点 的坐标为
的坐标为 .
.
同理可得点 的坐标为
的坐标为 .
.
∴
 .
.
∴
 . 设线段
. 设线段 的中点坐标为
的中点坐标为 ,
,
则
 .
.
∴以线段 为直径的圆的方程为
为直径的圆的方程为
 .
.
展开得
令 ,得
,得 ,解得
,解得 或
或 .
.
∴以线段 为直径的圆恒过两个定点
为直径的圆恒过两个定点 .
.
【思路点拨】(I)根据抛物线的定义可知曲线为抛物线;(II)联立直线方程可找出两交点之间的关系,求出ST的中点,建立以ST为直径的圆的方程,利用中点坐标的关系表示出圆的方程,可知有两个定点.

 阅读快车系列答案
阅读快车系列答案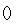 R).若z1z2为实数,则a的值为 .
R).若z1z2为实数,则a的值为 . 、
、 之间的距离为
之间的距离为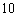 米.
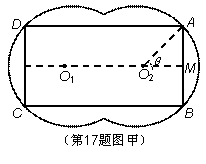
米. 1)如图甲,在花坛中建矩形喷泉,四个顶点
1)如图甲,在花坛中建矩形喷泉,四个顶点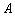 ,
,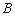 ,
,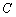 ,
,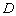 均在圆弧上,
均在圆弧上,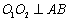 于点
于点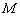 .设
.设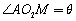 ,求矩形的宽
,求矩形的宽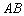 为多少时,可使喷泉
为多少时,可使喷泉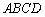 的面积最大;
的面积最大; ,
,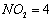 米.若
米.若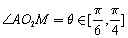 ,求喷泉的面积的取值范围.
,求喷泉的面积的取值范围.
 及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为
及其三视图中的正(主)视图和侧(左)视图如图所示,则棱SB的长为 B.
B.  C.
C.  D.
D. 

 .如果A中元素
.如果A中元素 满足
满足 ,就称A为“复活集”,给出下列结论:
,就称A为“复活集”,给出下列结论: 是“复活集”;
是“复活集”; 是“复活集”,则
是“复活集”,则 ;
; 不可能是“复活集”;
不可能是“复活集”; ,则“复活集”A有且只有一个,且
,则“复活集”A有且只有一个,且 .
. 是首项为
是首项为 ,公差为
,公差为 的等差数列,若数列
的等差数列,若数列 是等比数列,则其公比为( )
是等比数列,则其公比为( )






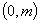 间的整数
间的整数 为分子,以
为分子,以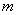 为分母组成分数集合
为分母组成分数集合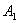 ,其所有元素和为
,其所有元素和为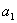 ;以
;以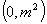 间的整数
间的整数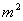 为分母组成不属于集合
为分母组成不属于集合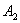 ,其所有元素和为
,其所有元素和为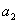 ;……,依次类推以
;……,依次类推以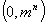 间的整数
间的整数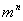 为分母组成不属于
为分母组成不属于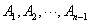 的分数集合
的分数集合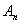 ,其所有元素和为
,其所有元素和为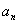 ;则
;则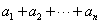 =________.
=________. 的圆心到直线
的圆心到直线
 (
( )的距离为
)的距离为 ,则
,则 .
. 的边长是3,
的边长是3, 是
是 上的点,BD=1,则
上的点,BD=1,则 =
= B.
B. C.
C. D.
D.