题目内容
已知有限集 .如果A中元素
.如果A中元素 满足
满足 ,就称A为“复活集”,给出下列结论:
,就称A为“复活集”,给出下列结论:
①集合 是“复活集”;
是“复活集”;
② 是“复活集”,则
是“复活集”,则 ;
;
③ 不可能是“复活集”;
不可能是“复活集”;
④若 ,则“复活集”A有且只有一个,且
,则“复活集”A有且只有一个,且 .
.
其中正确的结论是___________.(填上你认为所有正确的结论序号)
①③④解析 :解:易判断①是正确的;
②不妨设a1+a2=a1a2=t,则由韦达定理知a1,a2是一元二次方程x2-tx+t=0的两个根,由Δ>0,可得t<0,或t>4,故②错;
③不妨设A中a1<a2<a3<…<an,由a1a2…an=a1+a2+…+an<nan,得 <n,当n=2时,即有a1<2,∴a1=1,于是1+a2=a2,a2无解,即不存在满足条件的“复活集”A,故③正确;当n=3时,a1a2<3,故只能a1=1,a2=2,求得a3=3,于是“复活集”A只有一个,为{1,2,3}.当n≥4时,由
<n,当n=2时,即有a1<2,∴a1=1,于是1+a2=a2,a2无解,即不存在满足条件的“复活集”A,故③正确;当n=3时,a1a2<3,故只能a1=1,a2=2,求得a3=3,于是“复活集”A只有一个,为{1,2,3}.当n≥4时,由 ≥1×2×3×…×(n-1),即有n>(n-1)!,也就是说“复活集”A存在的必要条件是n>(n-1)!,事实上,(n-1)!≥(n-1)(n-2)=n2-3n+2=(n-2)2-2+n>2,矛盾,∴当n≥4时不存在复活集A,故④正确.
≥1×2×3×…×(n-1),即有n>(n-1)!,也就是说“复活集”A存在的必要条件是n>(n-1)!,事实上,(n-1)!≥(n-1)(n-2)=n2-3n+2=(n-2)2-2+n>2,矛盾,∴当n≥4时不存在复活集A,故④正确.
【思路点拨】根据已知中“复活集”的定义,结合韦达定理及反证法,逐一判断四个结论的正误,进而可得答案.

练习册系列答案
相关题目
 。
。 的解析式,最小值和最小正周期;
的解析式,最小值和最小正周期; 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值。
的值。  ,
, ,
, 满足
满足 ,
, ,
, ,
,  ,则
,则 的最小值为 .
的最小值为 . ,则“
,则“ ”是“
”是“ ”的
”的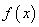 是定义在R上的偶函数,且
是定义在R上的偶函数,且 时,
时, ,若在区间
,若在区间 内,函数
内,函数 恰有1个零点,则实数
恰有1个零点,则实数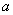 的取值范围是
的取值范围是 B.
B. C.
C.  D.
D. 
 ,过点F且与直线
,过点F且与直线 相切的动圆圆心为点M,记点M的轨迹为曲线E.
相切的动圆圆心为点M,记点M的轨迹为曲线E.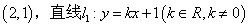 ,与曲线E相交于B,C两点,直线AB,AC分别交直线
,与曲线E相交于B,C两点,直线AB,AC分别交直线 的无穷等比数列
的无穷等比数列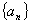
 的各项和等于4,则这个数列
的各项和等于4,则这个数列 是公差为2的等差数列,若
是公差为2的等差数列,若 是
是 和
和 的等比中项,则
的等比中项,则 =________.
=________. 名学生分别安排到甲、乙,丙三地参加社会实践活动,每个地方至少安排一名学生参加,则不同的安排方案共有
名学生分别安排到甲、乙,丙三地参加社会实践活动,每个地方至少安排一名学生参加,则不同的安排方案共有